Question Number 161323 by mnjuly1970 last updated on 16/Dec/21
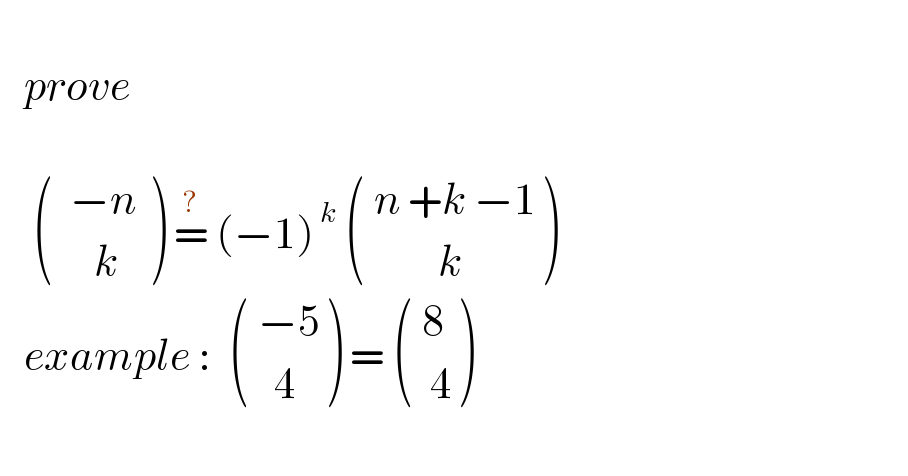
$$ \\ $$$$\:\:\:{prove} \\ $$$$ \\ $$$$\:\:\:\:\begin{pmatrix}{\:\:−{n}\:}\\{\:\:\:\:\:{k}}\end{pmatrix}\:\overset{?} {=}\:\left(−\mathrm{1}\right)^{\:{k}} \:\begin{pmatrix}{\:{n}\:+{k}\:−\mathrm{1}}\\{\:\:\:\:\:\:\:\:\:{k}}\end{pmatrix} \\ $$$$\:\:\:{example}\::\:\:\begin{pmatrix}{\:−\mathrm{5}}\\{\:\:\:\mathrm{4}}\end{pmatrix}\:=\:\begin{pmatrix}{\:\mathrm{8}}\\{\:\:\mathrm{4}}\end{pmatrix} \\ $$$$\:\:\:\:\:\:\: \\ $$
Commented by mr W last updated on 16/Dec/21
![(1+x)^m =Σ_(k=0) ^m C_k ^m x^k C_k ^m is the coef. of x^k term in (1+x)^m with m=−n (1+x)^(−n) =(1/([1−(−x)]^n )) =Σ_(k=0) ^∞ C_k ^(n+k−1) (−x)^k =Σ_(k=0) ^∞ (−1)^k C_k ^(k+n−1) x^k ⇒C_k ^m =C_k ^(−n) =(−1)^k C_k ^(k+n−1) =(−1)^k C_(n−1) ^(k+n−1)](https://www.tinkutara.com/question/Q161351.png)
$$\left(\mathrm{1}+{x}\right)^{{m}} =\underset{{k}=\mathrm{0}} {\overset{{m}} {\sum}}{C}_{{k}} ^{{m}} {x}^{{k}} \\ $$$${C}_{{k}} ^{{m}} \:{is}\:{the}\:{coef}.\:{of}\:{x}^{{k}} \:{term}\:{in}\:\left(\mathrm{1}+{x}\right)^{{m}} \\ $$$$ \\ $$$${with}\:{m}=−{n} \\ $$$$\left(\mathrm{1}+{x}\right)^{−{n}} \\ $$$$=\frac{\mathrm{1}}{\left[\mathrm{1}−\left(−{x}\right)\right]^{{n}} } \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{{k}} ^{{n}+{k}−\mathrm{1}} \left(−{x}\right)^{{k}} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}} {C}_{{k}} ^{{k}+{n}−\mathrm{1}} {x}^{{k}} \\ $$$$\Rightarrow{C}_{{k}} ^{{m}} ={C}_{{k}} ^{−{n}} =\left(−\mathrm{1}\right)^{{k}} {C}_{{k}} ^{{k}+{n}−\mathrm{1}} =\left(−\mathrm{1}\right)^{{k}} {C}_{{n}−\mathrm{1}} ^{{k}+{n}−\mathrm{1}} \\ $$
Commented by mnjuly1970 last updated on 17/Dec/21
$$\:\:\:{thanks}\:{alot}\:\:{sir}\:\:{W} \\ $$
Commented by Tawa11 last updated on 17/Dec/21

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Answered by mindispower last updated on 18/Dec/21

$$\begin{pmatrix}{−{n}}\\{{k}}\end{pmatrix}=\underset{{x}\rightarrow{n}} {\mathrm{lim}}\begin{pmatrix}{−{x}}\\{\:\:\:\:\:{k}}\end{pmatrix}=\underset{{x}\rightarrow{n}} {\mathrm{lim}}.\frac{\Gamma\left(\mathrm{1}−{x}\right)}{\Gamma\left(\mathrm{1}+{k}\right)\Gamma\left(−{x}−{k}+\mathrm{1}\right)} \\ $$$$\Gamma\left(\mathrm{1}−{a}\right)=\frac{\pi}{{sin}\left(\pi{a}\right)\Gamma\left({a}\right)} \\ $$$$=\underset{{x}\rightarrow{n}} {\mathrm{lim}}.\frac{\pi\Gamma\left({x}+{k}\right){sin}\left(\pi\left({n}+{k}\right)\right)}{{sin}\left(\pi{x}\right)\Gamma\left(\mathrm{1}+\mathrm{k}\right)\pi.\Gamma\left({x}\right)} \\ $$$${sin}\left({k}\pi+\pi{x}\right)=\left(−\mathrm{1}\right)^{{k}} {sin}\left(\pi{x}\right) \\ $$$$\Leftrightarrow\underset{{x}\rightarrow{n}} {\mathrm{lim}}\frac{\left(−\mathrm{1}\right)^{{k}} \Gamma\left({x}+{k}\right){sin}\left(\pi{x}\right)}{\Gamma\left(\mathrm{1}+{k}\right)\Gamma\left({x}\right).{sin}\left(\pi{x}\right)} \\ $$$${now}\:{use}\:{that}\:{x}\rightarrow\Gamma\left({x}\right),{continus}\:{fonction}\:{for} \\ $$$${x}>\mathrm{0}\:“\underset{{x}\rightarrow{n}} {\mathrm{lim}}\Gamma\left({x}\right)=\Gamma\left({n}\right)'' \\ $$$$=\left(−\mathrm{1}\right)^{{k}} .\frac{\Gamma\left({n}+{k}\right)}{\Gamma\left(\mathrm{1}+{k}\right).\Gamma\left({n}\right)}=\frac{\left({n}+{k}−\mathrm{1}\right)!}{{k}!.\left({n}−\mathrm{1}\right)!}\left(−\mathrm{1}\right)^{{k}} \\ $$$$=\left(−\mathrm{1}\right)^{{k}} \begin{pmatrix}{{n}+{k}−\mathrm{1}}\\{\:\:\:{k}}\end{pmatrix} \\ $$
Commented by mnjuly1970 last updated on 21/Dec/21
$$\:\:{very}\:{nice}\:{sir}\:{power}… \\ $$
Commented by mindispower last updated on 28/Dec/21

$${pleasur}\:{sir}\:{sorry}\:{problems}\:{withe}\:{my}\:{phone} \\ $$$${verry}\:{hard}\:{to}\left[{write}\:{answer}\:{or}\:{respend}\right. \\ $$
