Question Number 18397 by geovane10math last updated on 20/Jul/17
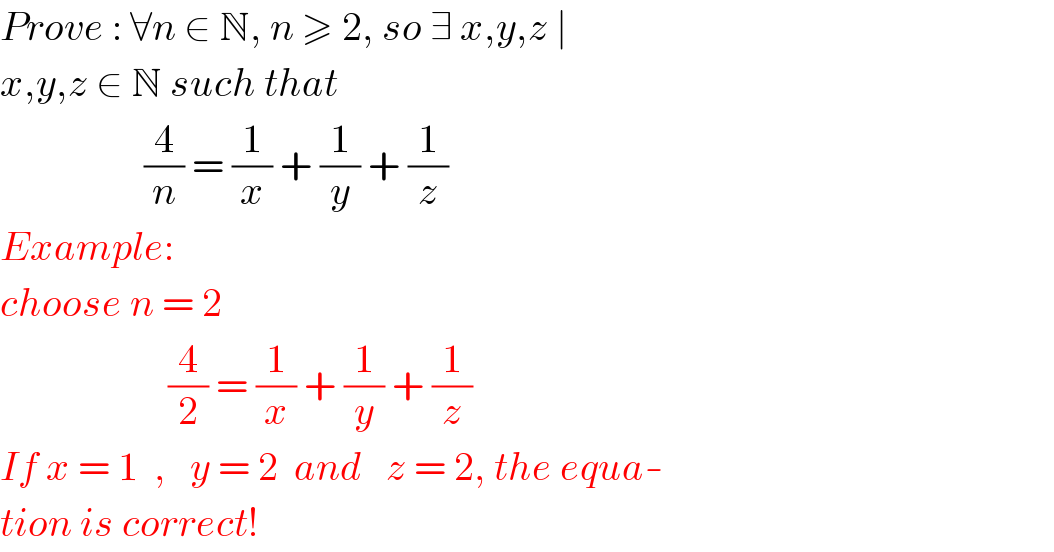
$${Prove}\::\:\forall{n}\:\in\:\mathbb{N},\:{n}\:\geqslant\:\mathrm{2},\:{so}\:\exists\:{x},{y},{z}\:\mid\: \\ $$$${x},{y},{z}\:\in\:\mathbb{N}\:{such}\:{that}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{4}}{{n}}\:=\:\frac{\mathrm{1}}{{x}}\:+\:\frac{\mathrm{1}}{{y}}\:+\:\frac{\mathrm{1}}{{z}} \\ $$$${Example}: \\ $$$${choose}\:{n}\:=\:\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{4}}{\mathrm{2}}\:=\:\frac{\mathrm{1}}{{x}}\:+\:\frac{\mathrm{1}}{{y}}\:+\:\frac{\mathrm{1}}{{z}} \\ $$$${If}\:{x}\:=\:\mathrm{1}\:\:,\:\:\:{y}\:=\:\mathrm{2}\:\:{and}\:\:\:{z}\:=\:\mathrm{2},\:{the}\:{equa}- \\ $$$${tion}\:{is}\:{correct}! \\ $$
