Question Number 163134 by mnjuly1970 last updated on 04/Jan/22
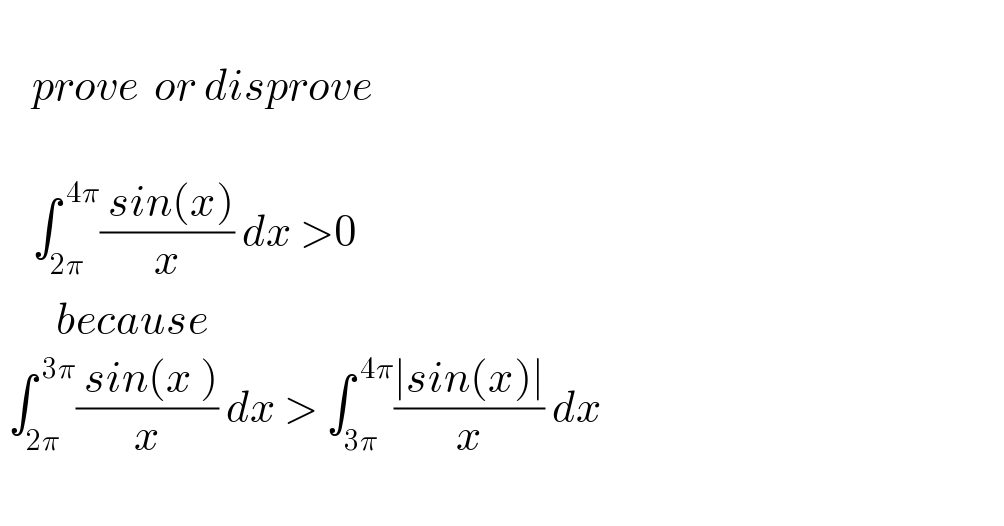
$$ \\ $$$$\:\:\:\:{prove}\:\:{or}\:{disprove} \\ $$$$ \\ $$$$\:\:\:\:\int_{\mathrm{2}\pi} ^{\:\mathrm{4}\pi} \frac{\:{sin}\left({x}\right)}{{x}}\:{dx}\:>\mathrm{0} \\ $$$$\:\:\:\:\:\:\:{because} \\ $$$$\:\int_{\mathrm{2}\pi} ^{\:\mathrm{3}\pi} \frac{\:{sin}\left({x}\:\right)}{{x}}\:{dx}\:>\:\int_{\mathrm{3}\pi} ^{\:\mathrm{4}\pi} \frac{\mid{sin}\left({x}\right)\mid}{{x}}\:{dx} \\ $$$$ \\ $$
Answered by mindispower last updated on 04/Jan/22
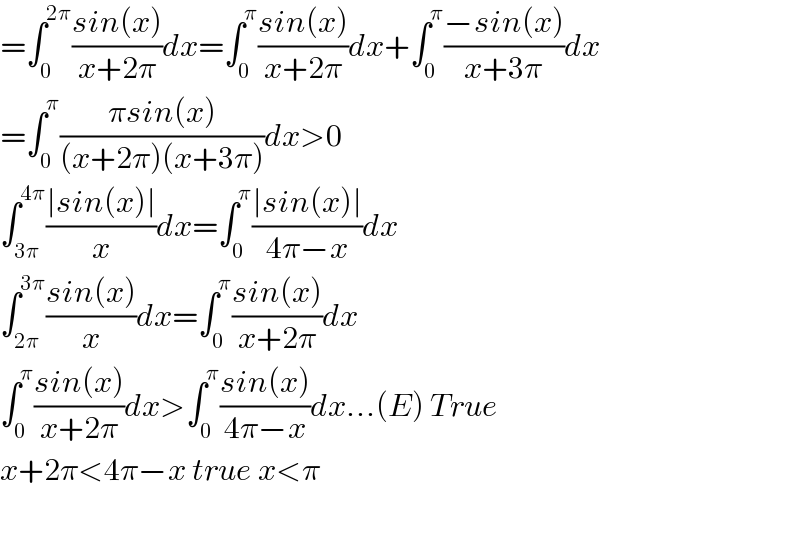
$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{{sin}\left({x}\right)}{{x}+\mathrm{2}\pi}{dx}=\int_{\mathrm{0}} ^{\pi} \frac{{sin}\left({x}\right)}{{x}+\mathrm{2}\pi}{dx}+\int_{\mathrm{0}} ^{\pi} \frac{−{sin}\left({x}\right)}{{x}+\mathrm{3}\pi}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \frac{\pi{sin}\left({x}\right)}{\left({x}+\mathrm{2}\pi\right)\left({x}+\mathrm{3}\pi\right)}{dx}>\mathrm{0} \\ $$$$\int_{\mathrm{3}\pi} ^{\mathrm{4}\pi} \frac{\mid{sin}\left({x}\right)\mid}{{x}}{dx}=\int_{\mathrm{0}} ^{\pi} \frac{\mid{sin}\left({x}\right)\mid}{\mathrm{4}\pi−{x}}{dx} \\ $$$$\int_{\mathrm{2}\pi} ^{\mathrm{3}\pi} \frac{{sin}\left({x}\right)}{{x}}{dx}=\int_{\mathrm{0}} ^{\pi} \frac{{sin}\left({x}\right)}{{x}+\mathrm{2}\pi}{dx} \\ $$$$\int_{\mathrm{0}} ^{\pi} \frac{{sin}\left({x}\right)}{{x}+\mathrm{2}\pi}{dx}>\int_{\mathrm{0}} ^{\pi} \frac{{sin}\left({x}\right)}{\mathrm{4}\pi−{x}}{dx}…\left({E}\right)\:{True} \\ $$$${x}+\mathrm{2}\pi<\mathrm{4}\pi−{x}\:{true}\:{x}<\pi \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 04/Jan/22
$$\:\:\:{grateful}\:{sir}\:{power}\:\:{perfect} \\ $$
Commented by mindispower last updated on 04/Jan/22
$${pleasur}\:{sir}\:{have}\:{nice}\:{day} \\ $$
