Prove-or-disprove-that-2-101-n-n-101-

Question Number 65214 by naka3546 last updated on 26/Jul/19

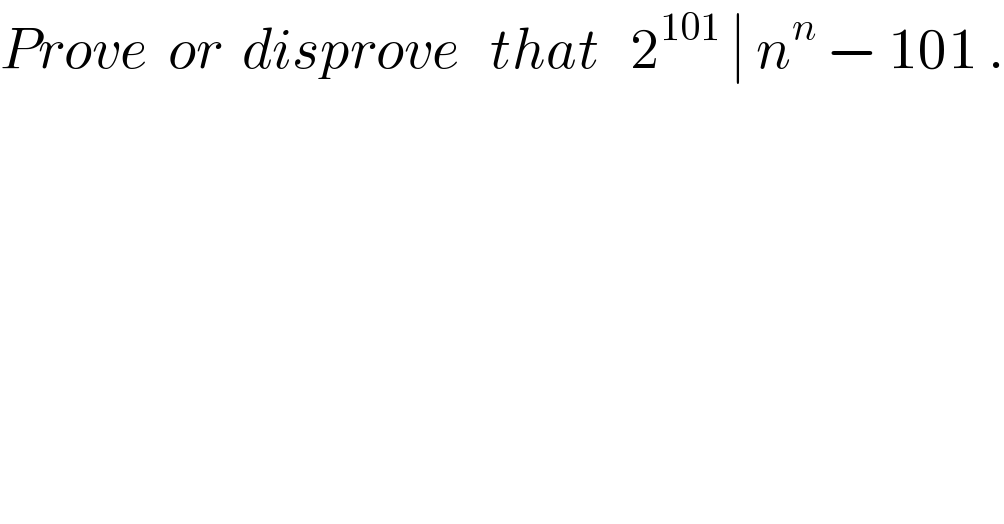
P r o v e o r d i s p r o v e t h a t 2^{101} ∣ n^{n} - 101 .

Commented by naka3546 last updated on 26/Jul/19

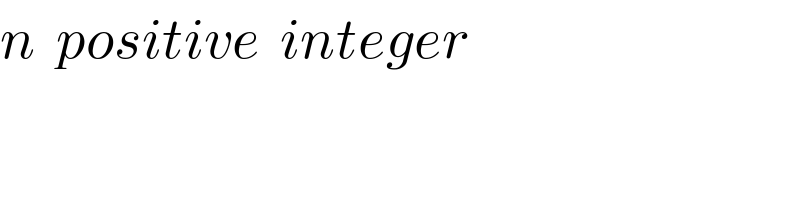
n p o s i t i v e i n t e g e r

Commented by Rasheed.Sindhi last updated on 27/Jul/19

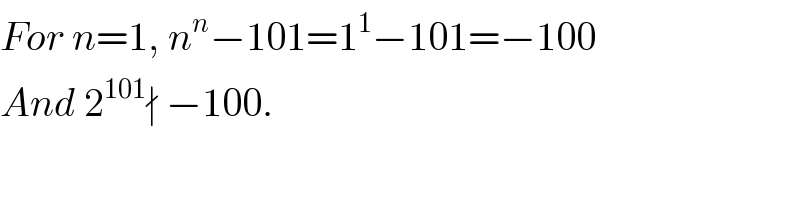
F o r n = 1, n^{n} - 101 = 1^{1} - 101 = - 100

A n d 2^{101} ∤ - 100 .

Commented by naka3546 last updated on 27/Jul/19

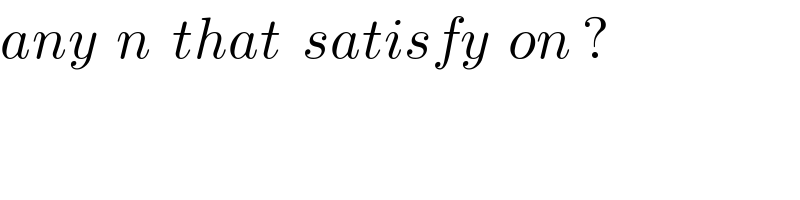
a n y n t h a t s a t i s f y o n ?

Answered by MJS last updated on 27/Jul/19

n^{n} - 101 ⩾ 2^{101} \Rightarrow n ⩾ 2^{101} + 101 = 2 535 301 200 456 458 802 993 406 410 853

n^{n} - 101 = m \times 2^{101}

n^{n} - 101 = 2 m \times 2^{100}

n^{n} - 101 = 2 l

n^{n} = 2 l + 101

n^{n} = 2 (l + 50) + 1

n^{n} = 2 k + 1 \Rightarrow {it}^{'} s not true for even n

2^{101} - 101 = 7^{2} \times 263 201 \times 196 582 994 842 884 397 808 597 =

= p^{2} q r

n^{n} = m \times p^{2} q r

m = \frac{n^{n}}{p^{2} q r} = \frac{{(p^{α} q^{β} r^{γ})}^{(p^{α} q^{β} r^{γ})}}{p^{2} q r} =

= p^{α p^{α} q^{β} r^{γ} - 2} q^{β p^{α} q^{β} r^{γ} - 1} r^{γ p^{α} q^{β} r^{γ} - 1}

the smallest number m is the one with

α = β = γ = 1

m_{m i n} = p^{p q r - 2} q^{p q r - 1} r^{p q r - 1} \approx 10^{(10^{31})}

Facebook Tweet Pin