Prove-or-disprove-the-foolowing-n-1-1-n-2-n-2-2-e-n-2-x-n-1-e-n-2-x-

Question Number 150539 by mathdanisur last updated on 13/Aug/21

Prove or disprove the foolowing: Σ_(n=1) ^∞ (−1)^((n^2 +n+2)/2) e^(−𝛑n^2 x) = Σ_(n=1) ^∞ e^(−𝛑n^2 x)

$$\mathrm{Prove}\:\mathrm{or}\:\mathrm{disprove}\:\mathrm{the}\:\mathrm{foolowing}: \\ $$$$\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\frac{\boldsymbol{\mathrm{n}}^{\mathrm{2}} +\boldsymbol{\mathrm{n}}+\mathrm{2}}{\mathrm{2}}} \:\mathrm{e}^{−\boldsymbol{\pi\mathrm{n}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}} \:=\:\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{e}^{−\boldsymbol{\pi\mathrm{n}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}} \\ $$

Answered by Math_Freak last updated on 13/Aug/21

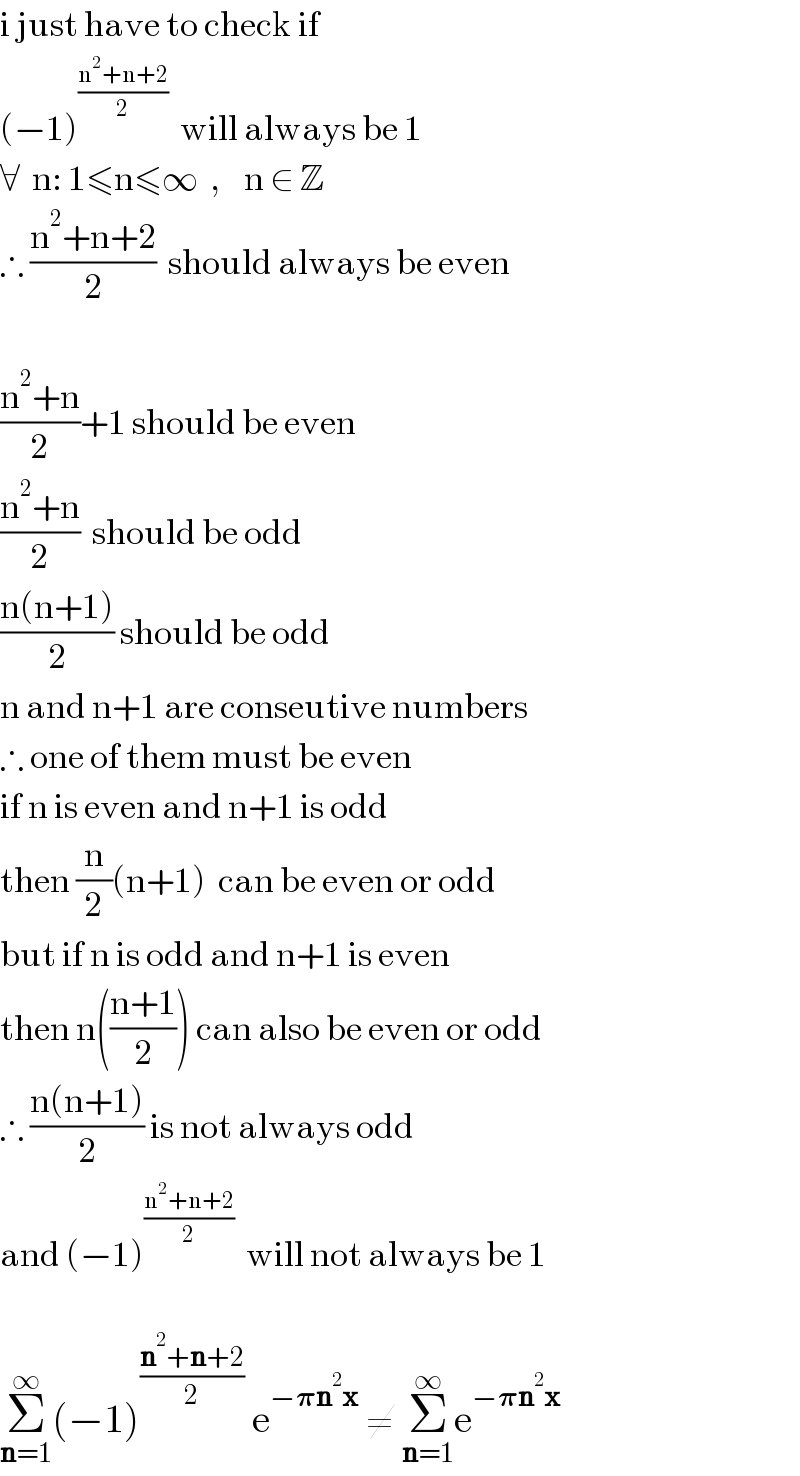
i just have to check if (−1)^((n^2 +n+2)/2) will always be 1 ∀ n: 1≤n≤∞ , n ∈ Z ∴ ((n^2 +n+2)/2) should always be even ((n^2 +n)/2)+1 should be even ((n^2 +n)/2) should be odd ((n(n+1))/2) should be odd n and n+1 are conseutive numbers ∴ one of them must be even if n is even and n+1 is odd then (n/2)(n+1) can be even or odd but if n is odd and n+1 is even then n(((n+1)/2)) can also be even or odd ∴ ((n(n+1))/2) is not always odd and (−1)^((n^2 +n+2)/2) will not always be 1 Σ_(n=1) ^∞ (−1)^((n^2 +n+2)/2) e^(−𝛑n^2 x) ≠ Σ_(n=1) ^∞ e^(−𝛑n^2 x)

$$\mathrm{i}\:\mathrm{just}\:\mathrm{have}\:\mathrm{to}\:\mathrm{check}\:\mathrm{if} \\ $$$$\left(−\mathrm{1}\right)^{\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{n}+\mathrm{2}}{\mathrm{2}}} \:\:\mathrm{will}\:\mathrm{always}\:\mathrm{be}\:\mathrm{1} \\ $$$$\forall\:\:\mathrm{n}:\:\mathrm{1}\leqslant\mathrm{n}\leqslant\infty\:\:,\:\:\:\:\mathrm{n}\:\in\:\mathbb{Z} \\ $$$$\therefore\:\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{n}+\mathrm{2}}{\mathrm{2}}\:\:\mathrm{should}\:\mathrm{always}\:\mathrm{be}\:\mathrm{even} \\ $$$$ \\ $$$$\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{n}}{\mathrm{2}}+\mathrm{1}\:\mathrm{should}\:\mathrm{be}\:\mathrm{even} \\ $$$$\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{n}}{\mathrm{2}}\:\:\mathrm{should}\:\mathrm{be}\:\mathrm{odd} \\ $$$$\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}}\:\mathrm{should}\:\mathrm{be}\:\mathrm{odd} \\ $$$$\mathrm{n}\:\mathrm{and}\:\mathrm{n}+\mathrm{1}\:\mathrm{are}\:\mathrm{conseutive}\:\mathrm{numbers} \\ $$$$\therefore\:\mathrm{one}\:\mathrm{of}\:\mathrm{them}\:\mathrm{must}\:\mathrm{be}\:\mathrm{even} \\ $$$$\mathrm{if}\:\mathrm{n}\:\mathrm{is}\:\mathrm{even}\:\mathrm{and}\:\mathrm{n}+\mathrm{1}\:\mathrm{is}\:\mathrm{odd} \\ $$$$\mathrm{then}\:\frac{\mathrm{n}}{\mathrm{2}}\left(\mathrm{n}+\mathrm{1}\right)\:\:\mathrm{can}\:\mathrm{be}\:\mathrm{even}\:\mathrm{or}\:\mathrm{odd} \\ $$$$\mathrm{but}\:\mathrm{if}\:\mathrm{n}\:\mathrm{is}\:\mathrm{odd}\:\mathrm{and}\:\mathrm{n}+\mathrm{1}\:\mathrm{is}\:\mathrm{even} \\ $$$$\mathrm{then}\:\mathrm{n}\left(\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}}\right)\:\mathrm{can}\:\mathrm{also}\:\mathrm{be}\:\mathrm{even}\:\mathrm{or}\:\mathrm{odd} \\ $$$$\therefore\:\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}}\:\mathrm{is}\:\mathrm{not}\:\mathrm{always}\:\mathrm{odd} \\ $$$$\mathrm{and}\:\left(−\mathrm{1}\right)^{\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{n}+\mathrm{2}}{\mathrm{2}}} \:\:\mathrm{will}\:\mathrm{not}\:\mathrm{always}\:\mathrm{be}\:\mathrm{1} \\ $$$$ \\ $$$$\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\frac{\boldsymbol{\mathrm{n}}^{\mathrm{2}} +\boldsymbol{\mathrm{n}}+\mathrm{2}}{\mathrm{2}}} \:\mathrm{e}^{−\boldsymbol{\pi\mathrm{n}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}} \:\neq\:\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{e}^{−\boldsymbol{\pi\mathrm{n}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}} \\ $$

Commented by mathdanisur last updated on 14/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser} \\ $$

Facebook Tweet Pin

Prove-or-disprove-the-foolowing-n-1-1-n-2-n-2-2-e-n-2-x-n-1-e-n-2-x-

Leave a Reply Cancel reply