Menu Close

Prove-sin-3pi-10-1-5-4-

Tinku Tara 0 Comments
Pin




Question Number 18584 by 433 last updated on 25/Jul/17
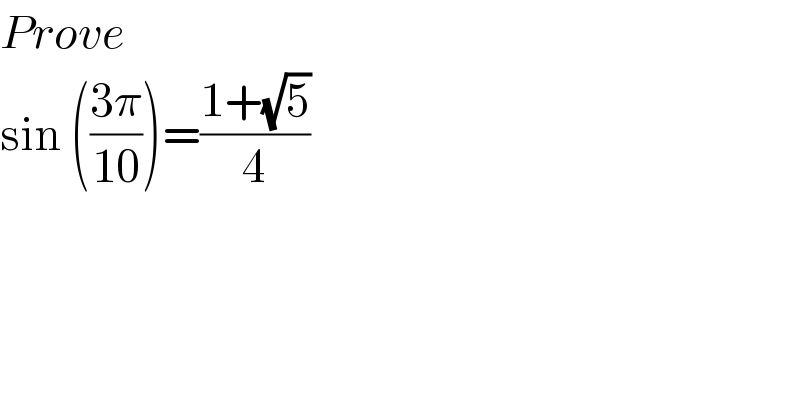
Prove sin (((3π)/(10)))=((1+(√5))/4)
Provesin(3π10)=1+54
Answered by Tinkutara last updated on 25/Jul/17
sin 54° = cos 36° = 1 − 2 sin^2 18° = 1 − ((3 − (√5))/4) = (((√5) + 1)/4) [∵ sin 18° = (((√5) − 1)/4)]
sin54°=cos36°=1−2sin218°=1−3−54=5+14[∵sin18°=5−14]

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *