Menu Close

prove-sin-a-sin-b-sin-c-4cos-a-2-cos-b-2-cos-c-2-

Tinku Tara 0 Comments
Pin




Question Number 81760 by jagoll last updated on 15/Feb/20
prove sin a+sin b+sin c =? 4cos ((a/2))cos ((b/2))cos ((c/2))
$${prove}\: \\ $$$$\mathrm{sin}\:{a}+\mathrm{sin}\:{b}+\mathrm{sin}\:{c}\:=? \\ $$$$\mathrm{4cos}\:\left(\frac{{a}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{b}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{c}}{\mathrm{2}}\right) \\ $$
Commented by jagoll last updated on 15/Feb/20
thank you
$${thank}\:{you} \\ $$
Commented by john santu last updated on 15/Feb/20
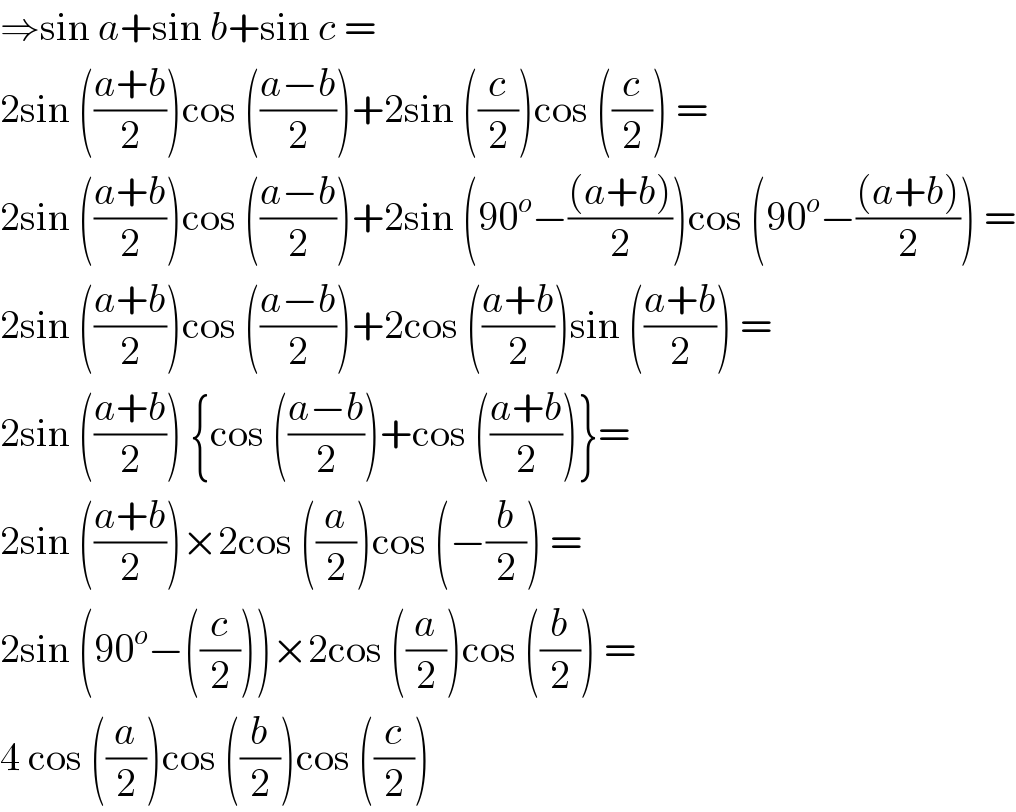
⇒sin a+sin b+sin c = 2sin (((a+b)/2))cos (((a−b)/2))+2sin ((c/2))cos ((c/2)) = 2sin (((a+b)/2))cos (((a−b)/2))+2sin (90^o −(((a+b))/2))cos (90^o −(((a+b))/2)) = 2sin (((a+b)/2))cos (((a−b)/2))+2cos (((a+b)/2))sin (((a+b)/2)) = 2sin (((a+b)/2)) {cos (((a−b)/2))+cos (((a+b)/2))}= 2sin (((a+b)/2))×2cos ((a/2))cos (−(b/2)) = 2sin (90^o −((c/2)))×2cos ((a/2))cos ((b/2)) = 4 cos ((a/2))cos ((b/2))cos ((c/2))
$$\Rightarrow\mathrm{sin}\:{a}+\mathrm{sin}\:{b}+\mathrm{sin}\:{c}\:= \\ $$$$\mathrm{2sin}\:\left(\frac{{a}+{b}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{a}−{b}}{\mathrm{2}}\right)+\mathrm{2sin}\:\left(\frac{{c}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{c}}{\mathrm{2}}\right)\:= \\ $$$$\mathrm{2sin}\:\left(\frac{{a}+{b}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{a}−{b}}{\mathrm{2}}\right)+\mathrm{2sin}\:\left(\mathrm{90}^{{o}} −\frac{\left({a}+{b}\right)}{\mathrm{2}}\right)\mathrm{cos}\:\left(\mathrm{90}^{{o}} −\frac{\left({a}+{b}\right)}{\mathrm{2}}\right)\:= \\ $$$$\mathrm{2sin}\:\left(\frac{{a}+{b}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{a}−{b}}{\mathrm{2}}\right)+\mathrm{2cos}\:\left(\frac{{a}+{b}}{\mathrm{2}}\right)\mathrm{sin}\:\left(\frac{{a}+{b}}{\mathrm{2}}\right)\:= \\ $$$$\mathrm{2sin}\:\left(\frac{{a}+{b}}{\mathrm{2}}\right)\:\left\{\mathrm{cos}\:\left(\frac{{a}−{b}}{\mathrm{2}}\right)+\mathrm{cos}\:\left(\frac{{a}+{b}}{\mathrm{2}}\right)\right\}= \\ $$$$\mathrm{2sin}\:\left(\frac{{a}+{b}}{\mathrm{2}}\right)×\mathrm{2cos}\:\left(\frac{{a}}{\mathrm{2}}\right)\mathrm{cos}\:\left(−\frac{{b}}{\mathrm{2}}\right)\:= \\ $$$$\mathrm{2sin}\:\left(\mathrm{90}^{{o}} −\left(\frac{{c}}{\mathrm{2}}\right)\right)×\mathrm{2cos}\:\left(\frac{{a}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{b}}{\mathrm{2}}\right)\:= \\ $$$$\mathrm{4}\:\mathrm{cos}\:\left(\frac{{a}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{b}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{c}}{\mathrm{2}}\right)\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *