Question Number 113151 by ZiYangLee last updated on 11/Sep/20
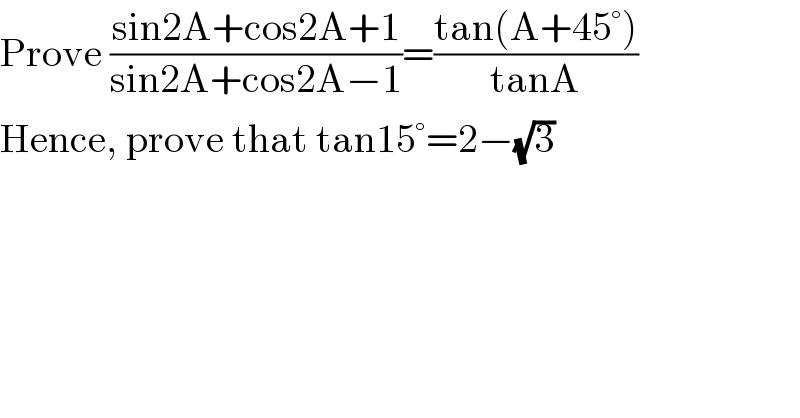
$$\mathrm{Prove}\:\frac{\mathrm{sin2A}+\mathrm{cos2A}+\mathrm{1}}{\mathrm{sin2A}+\mathrm{cos2A}−\mathrm{1}}=\frac{\mathrm{tan}\left(\mathrm{A}+\mathrm{45}°\right)}{\mathrm{tanA}} \\ $$$$\mathrm{Hence},\:\mathrm{prove}\:\mathrm{that}\:\mathrm{tan15}°=\mathrm{2}−\sqrt{\mathrm{3}} \\ $$
Commented by ZiYangLee last updated on 11/Sep/20
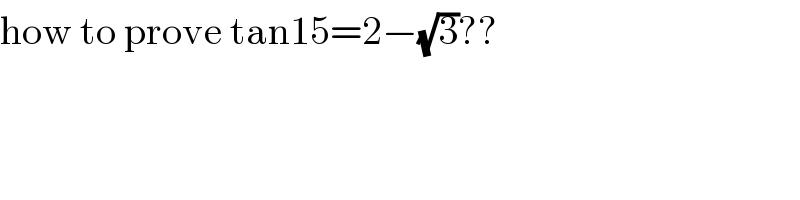
$$\mathrm{how}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{tan15}=\mathrm{2}−\sqrt{\mathrm{3}}?? \\ $$
Commented by Dwaipayan Shikari last updated on 11/Sep/20
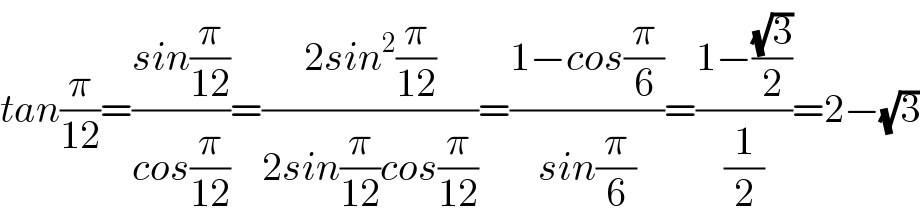
$${tan}\frac{\pi}{\mathrm{12}}=\frac{{sin}\frac{\pi}{\mathrm{12}}}{{cos}\frac{\pi}{\mathrm{12}}}=\frac{\mathrm{2}{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{12}}}{\mathrm{2}{sin}\frac{\pi}{\mathrm{12}}{cos}\frac{\pi}{\mathrm{12}}}=\frac{\mathrm{1}−{cos}\frac{\pi}{\mathrm{6}}}{{sin}\frac{\pi}{\mathrm{6}}}=\frac{\mathrm{1}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{\frac{\mathrm{1}}{\mathrm{2}}}=\mathrm{2}−\sqrt{\mathrm{3}} \\ $$
Commented by Dwaipayan Shikari last updated on 11/Sep/20

$${A}=−\frac{\pi}{\mathrm{6}}\: \\ $$
Commented by ZiYangLee last updated on 11/Sep/20

$$\mathrm{thanks}!!\:\mathrm{i}\:\mathrm{get}\:\mathrm{it}!!< \\ $$
Answered by som(math1967) last updated on 11/Sep/20

$$\frac{\mathrm{1}+\mathrm{sin2A}+\mathrm{cos2A}}{\mathrm{cos2A}−\left(\mathrm{1}−\mathrm{sin2A}\right)} \\ $$$$=\frac{\left(\mathrm{cosA}+\mathrm{sinA}\right)^{\mathrm{2}} +\left(\mathrm{cosA}+\mathrm{sinA}\right)\left(\mathrm{cosA}−\mathrm{sinA}\right)}{\left(\mathrm{cosA}+\mathrm{sinA}\right)\left(\mathrm{cosA}−\mathrm{sinA}\right)−\left(\mathrm{cosA}−\mathrm{sinA}\right)^{\mathrm{2}} } \\ $$$$=\frac{\left(\mathrm{cosA}+\mathrm{sinA}\right)\left(\mathrm{cosA}+\mathrm{sinA}+\mathrm{cosA}−\mathrm{sinA}\right)}{\left(\mathrm{cosA}−\mathrm{sinA}\right)\left(\mathrm{cosA}−\mathrm{sinA}−\mathrm{cosA}+\mathrm{sinA}\right)} \\ $$$$\frac{\left(\mathrm{cosA}+\mathrm{sinA}\right)\mathrm{2cosA}}{\left(\mathrm{cosA}−\mathrm{sinA}\right)\mathrm{2sinA}} \\ $$$$=\frac{\frac{\mathrm{cosA}+\mathrm{sinA}}{\mathrm{cosA}}}{\frac{\mathrm{cosA}−\mathrm{sinA}}{\mathrm{cosA}}}×\mathrm{cotA} \\ $$$$=\frac{\mathrm{1}+\mathrm{tanA}}{\mathrm{1}−\mathrm{tanA}}×\frac{\mathrm{1}}{\mathrm{tanA}} \\ $$$$=\frac{\mathrm{tan}\left(\mathrm{A}+\mathrm{45}°\right)}{\mathrm{tanA}}\:\:\bigstar \\ $$$$\bigstar\frac{\mathrm{1}+\mathrm{tanA}}{\mathrm{1}−\mathrm{tanA}}=\mathrm{tan}\left(\mathrm{A}+\mathrm{45}°\right) \\ $$$$ \\ $$
