Question Number 106726 by ZiYangLee last updated on 06/Aug/20
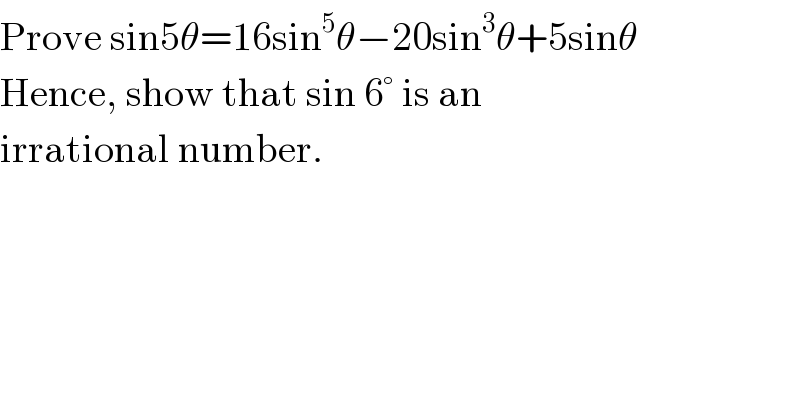
$$\mathrm{Prove}\:\mathrm{sin5}\theta=\mathrm{16sin}^{\mathrm{5}} \theta−\mathrm{20sin}^{\mathrm{3}} \theta+\mathrm{5sin}\theta \\ $$$$\mathrm{Hence},\:\mathrm{show}\:\mathrm{that}\:\mathrm{sin}\:\mathrm{6}°\:\mathrm{is}\:\mathrm{an} \\ $$$$\mathrm{irrational}\:\mathrm{number}.\: \\ $$
Answered by Ar Brandon last updated on 06/Aug/20
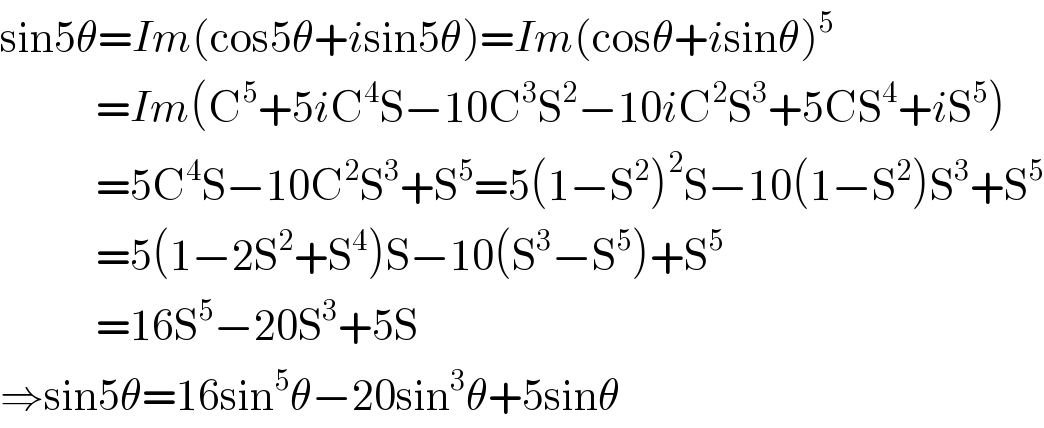
$$\mathrm{sin5}\theta={Im}\left(\mathrm{cos5}\theta+{i}\mathrm{sin5}\theta\right)={Im}\left(\mathrm{cos}\theta+{i}\mathrm{sin}\theta\right)^{\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:={Im}\left(\mathrm{C}^{\mathrm{5}} +\mathrm{5}{i}\mathrm{C}^{\mathrm{4}} \mathrm{S}−\mathrm{10C}^{\mathrm{3}} \mathrm{S}^{\mathrm{2}} −\mathrm{10}{i}\mathrm{C}^{\mathrm{2}} \mathrm{S}^{\mathrm{3}} +\mathrm{5CS}^{\mathrm{4}} +{i}\mathrm{S}^{\mathrm{5}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{5C}^{\mathrm{4}} \mathrm{S}−\mathrm{10C}^{\mathrm{2}} \mathrm{S}^{\mathrm{3}} +\mathrm{S}^{\mathrm{5}} =\mathrm{5}\left(\mathrm{1}−\mathrm{S}^{\mathrm{2}} \right)^{\mathrm{2}} \mathrm{S}−\mathrm{10}\left(\mathrm{1}−\mathrm{S}^{\mathrm{2}} \right)\mathrm{S}^{\mathrm{3}} +\mathrm{S}^{\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{5}\left(\mathrm{1}−\mathrm{2S}^{\mathrm{2}} +\mathrm{S}^{\mathrm{4}} \right)\mathrm{S}−\mathrm{10}\left(\mathrm{S}^{\mathrm{3}} −\mathrm{S}^{\mathrm{5}} \right)+\mathrm{S}^{\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{16S}^{\mathrm{5}} −\mathrm{20S}^{\mathrm{3}} +\mathrm{5S} \\ $$$$\Rightarrow\mathrm{sin5}\theta=\mathrm{16sin}^{\mathrm{5}} \theta−\mathrm{20sin}^{\mathrm{3}} \theta+\mathrm{5sin}\theta \\ $$
