Question Number 165072 by mathls last updated on 25/Jan/22
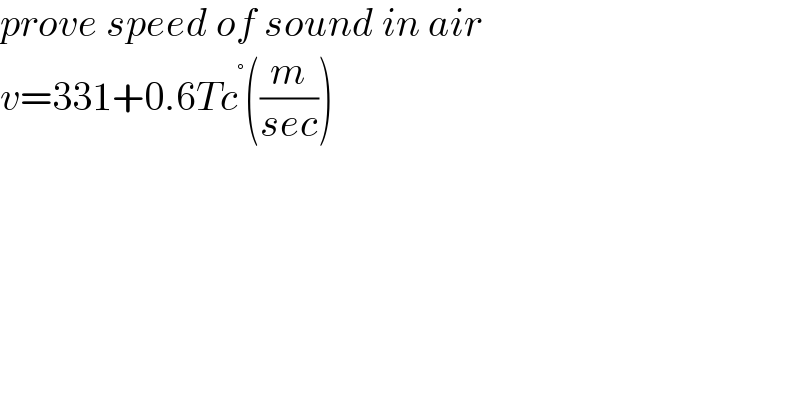
$${prove}\:{speed}\:{of}\:{sound}\:{in}\:{air} \\ $$$${v}=\mathrm{331}+\mathrm{0}.\mathrm{6}{Tc}^{°} \left(\frac{{m}}{{sec}}\right) \\ $$
Commented by mr W last updated on 25/Jan/22

$${can}\:{you}\:{prove}\:{that}\:{the}\:{Sun}\:{is}\:{larger} \\ $$$${than}\:{the}\:{Moon}?\:{can}\:{you}\:{prove}\:{that} \\ $$$${a}\:{year}\:{has}\:\mathrm{365}\:{days}? \\ $$$${these}\:{are}\:{facts}.\:{facts}\:{can}\:{not}\:{be}\:{proved} \\ $$$${and}\:{needn}'{t}\:{to}\:{be}\:{proved}. \\ $$$${the}\:{speed}\:{of}\:{sound}\:{in}\:{the}\:{air}\:{is}\:{also} \\ $$$${a}\:{fact}.\:{the}\:{speed}\:{in}\:{air}\:{is}\:{not}\:{a}\:{constant}, \\ $$$${this}\:{is}\:{also}\:{a}\:{fact}.\:{it}\:{depends}\:{on}\:{many} \\ $$$${many}\:{factors},\:{e}.{g}.\:{the}\:{temperature}, \\ $$$${the}\:{pressure},\:{the}\:{relative}\:{humidity}, \\ $$$${the}\:{polution},\:{and}\:{and}\:{and}.\:{the}\:{speeds} \\ $$$${of}\:{sound}\:{in}\:{air}\:{are}\:{facts},\:{the}\:{values} \\ $$$${are}\:{measured},\:{not}\:{calculated}!\:{the} \\ $$$${dependence}\:{of}\:{measured}\:{sound}\:{speed}\:{on}\:{the} \\ $$$${the}\:{temperature}\:{can}\:{be}\:{approximately} \\ $$$${described}\:{with}\:{v}=\mathrm{331}+\mathrm{0}.\mathrm{6}{T}.\:{but}\:{this} \\ $$$${is}\:{not}\:{a}\:{mathematical}\:{or}\:{physical} \\ $$$${theorem}\:{which}\:{you}\:{can}\:{prove}\:{or}\:{you} \\ $$$${can}\:{derivate}.\:{it}'{s}\:{just}\:{a}\:{approximation}\: \\ $$$${of}\:{facts}. \\ $$$${other}\:{people}\:{describe}\:{the}\:{same} \\ $$$${dependence}\:{with}\:{v}=\mathrm{20}.\mathrm{05}\sqrt{\mathrm{273}.\mathrm{16}+{T}}. \\ $$$${this}\:{is}\:{also}\:{only}\:{an}\:{approximation}. \\ $$$${maybe}\:{you}\:{can}\:{find}\:{even}\:{a}\:{better} \\ $$$${approximation}\:{in}\:{form}\:{of} \\ $$$${v}={aT}^{\mathrm{2}} +{bT}+{c}\sqrt[{\mathrm{3}}]{{T}}+{d}\:\mathrm{ln}\:\alpha{T}. \\ $$
Commented by mr W last updated on 25/Jan/22

$${as}\:{i}\:{have}\:{said}\:{the}\:{forum}\:{is}\:{not}\:{a} \\ $$$${good}\:{place}\:{for}\:{you}\:{to}\:{learn}\:{facts}\:{or} \\ $$$${elementary}\:{things}.\:{go}\:{to}\:{other}\:{places} \\ $$$${like}\:{google}! \\ $$
Commented by mathls last updated on 25/Jan/22
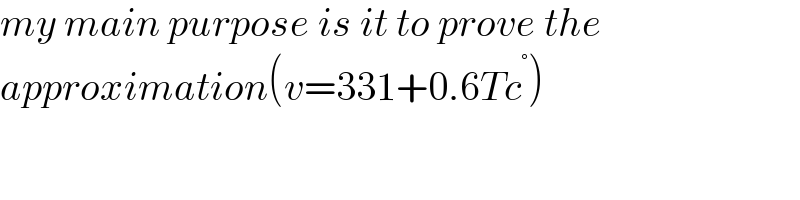
$${my}\:{main}\:{purpose}\:{is}\:{it}\:{to}\:{prove}\:{the} \\ $$$${approximation}\left({v}=\mathrm{331}+\mathrm{0}.\mathrm{6}{Tc}^{°} \right) \\ $$
Commented by mr W last updated on 25/Jan/22

$${you}\:{can}\:{not}\:{prove}\:{an}\:{approximation}! \\ $$$${as}\:{i}\:{have}\:{said},\:{you}\:{can}\:{even}\:{construct}\: \\ $$$${an}\:{approximation}\:{of}\:{your}\:{own}\:{for}\: \\ $$$${the}\:{same}\:{data}. \\ $$$${go}\:{to}\:{google}\:{and}\:{search}\:“{how}\:{to}\:{find} \\ $$$${curve}\:{of}\:{best}\:{fit}''. \\ $$
Commented by mathls last updated on 25/Jan/22
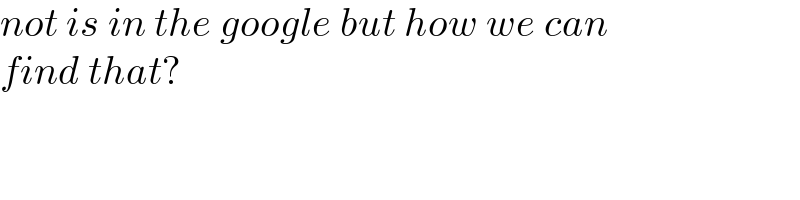
$${not}\:{is}\:{in}\:{the}\:{google}\:{but}\:{how}\:{we}\:{can} \\ $$$${find}\:{that}? \\ $$
Commented by mathls last updated on 26/Jan/22
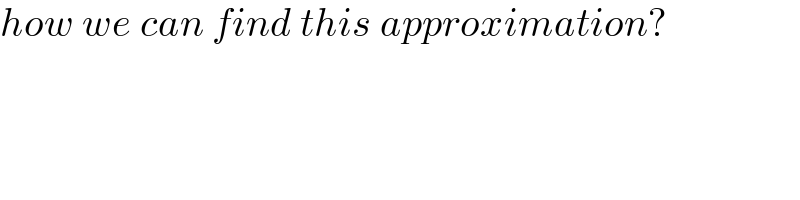
$${how}\:{we}\:{can}\:{find}\:{this}\:{approximation}? \\ $$
Commented by mr W last updated on 26/Jan/22

$${go}\:{to}\:{google}\:{and}\:{type}\:“{sound}\:{speed}\:{in} \\ $$$${air}''\:{and}\:{then}\:{just}\:{read},\:{read},\:{read}\:… \\ $$
Commented by mr W last updated on 26/Jan/22
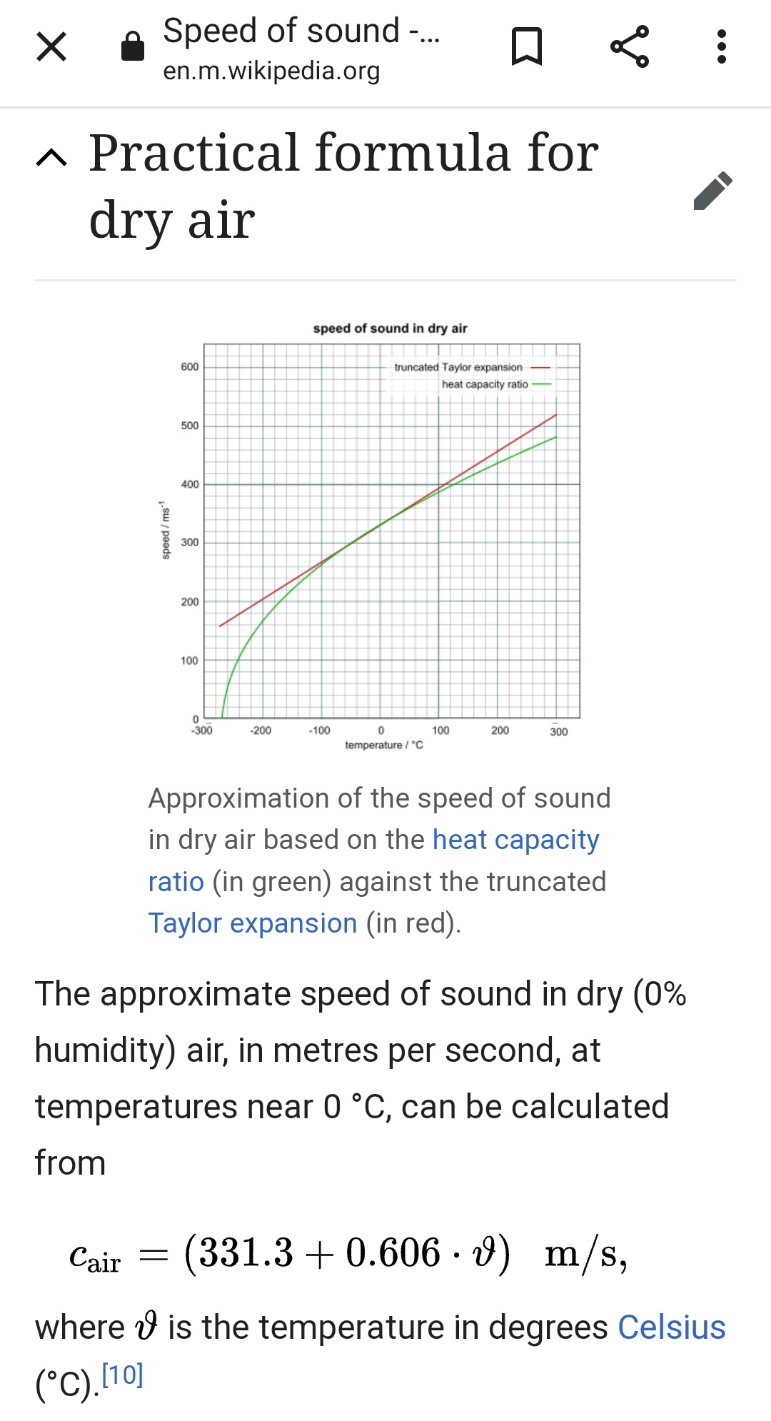
Commented by mr W last updated on 26/Jan/22

Commented by mr W last updated on 26/Jan/22

$${when}\:{i}\:{can}\:{find},\:{why}\:{can}\:{you}\:{not}\:{find}? \\ $$$${where}\:{are}\:{you}\:{from}?\:{is}\:{google}\: \\ $$$${restricted}\:{in}\:{your}\:{country}? \\ $$
Commented by Tinku Tara last updated on 26/Jan/22

$$\mathrm{For}\:\mathrm{theory}\:\mathrm{question}\:\mathrm{such}\:\mathrm{as}\:\mathrm{this}\:\mathrm{you} \\ $$$$\mathrm{will}\:\mathrm{find}\:\mathrm{google}\:\mathrm{search}\:\mathrm{gives}\:\mathrm{good} \\ $$$$\mathrm{answers}.\:\mathrm{For}\:\mathrm{maths}\:\mathrm{problems} \\ $$$$\mathrm{google}\:\mathrm{search}\:\mathrm{will}\:\mathrm{not}\:\mathrm{give}\:\mathrm{good}\:\mathrm{results}. \\ $$
Commented by mathls last updated on 26/Jan/22
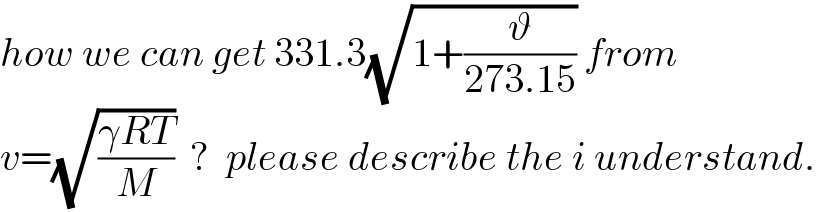
$${how}\:{we}\:{can}\:{get}\:\mathrm{331}.\mathrm{3}\sqrt{\mathrm{1}+\frac{\vartheta}{\mathrm{273}.\mathrm{15}}}\:{from} \\ $$$${v}=\sqrt{\frac{\gamma{RT}}{{M}}}\:\:?\:\:{please}\:{describe}\:{the}\:{i}\:{understand}. \\ $$
Commented by mathls last updated on 26/Jan/22
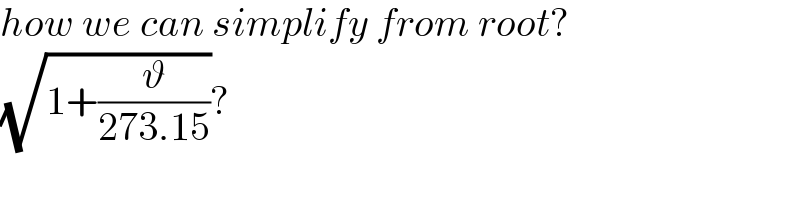
$${how}\:{we}\:{can}\:{simplify}\:{from}\:{root}? \\ $$$$\sqrt{\mathrm{1}+\frac{\vartheta}{\mathrm{273}.\mathrm{15}}}? \\ $$
Commented by mr W last updated on 26/Jan/22

$${have}\:{you}\:{read}\:{the}\:{article}\:{in}\: \\ $$$${wikipedia}? \\ $$$$\left.{A}\right)\:{no},\:{you}\:{havn}'{t}. \\ $$$$\Rightarrow\:{then}\:{you}\:{are}\:{too}\:{lazy}.\:{since}\:{i}\:{don}'{t}\: \\ $$$${like}\:{to}\:{lose}\:{my}\:{time}\:{for}\:{lazy}\:{people},\: \\ $$$${i}\:{won}'{t}\:{say}\:{anything}\:{more}. \\ $$$$\left.{B}\right)\:{yes},\:{you}\:{have},\:{but}\:{you}\:{still}\:{don}'{t}\: \\ $$$${understand}\:{the}\:{content}\:{there}. \\ $$$$\Rightarrow\:{then}\:{the}\:{thing}\:{is}\:{too}\:{high}\:{for}\:{your}\: \\ $$$${level}\:{at}\:{the}\:{moment}.\:{if}\:{you}\:{even}\:{don}'{t} \\ $$$${understand}\:{the}\:{explanation}\:{in}\:{the} \\ $$$${article},\:{which}\:{is}\:{very}\:{detailed}\:{and} \\ $$$${comprehensive},\:{then}\:{i}\:{can}\:{also}\:{not} \\ $$$${help}\:{you}\:{further},\:{because}\:{i}\:{can}'{t} \\ $$$${explain}\:{it}\:{better}\:{than}\:{the}\:{article}. \\ $$$${my}\:{suggestion}\:{is}\:{that}\:{you}\:{let}\:{the}\:{thing} \\ $$$${be}\:{and}\:{wait}\:{some}\:{time}\:{till}\:{you}\:{have}\: \\ $$$${learnt}\:{a}\:{little}\:{more}\:{in}\:{physics}\:{and}\: \\ $$$${mathematics},\:{for}\:{example}\:{what}\:{is}\: \\ $$$${absolute}\:{temperature}\:{and}\:{what}\:{is}\: \\ $$$${taylor}\:{expansion}\:{of}\:{a}\:{function}\:{etc}. \\ $$
