Question Number 34500 by Neelam last updated on 07/May/18
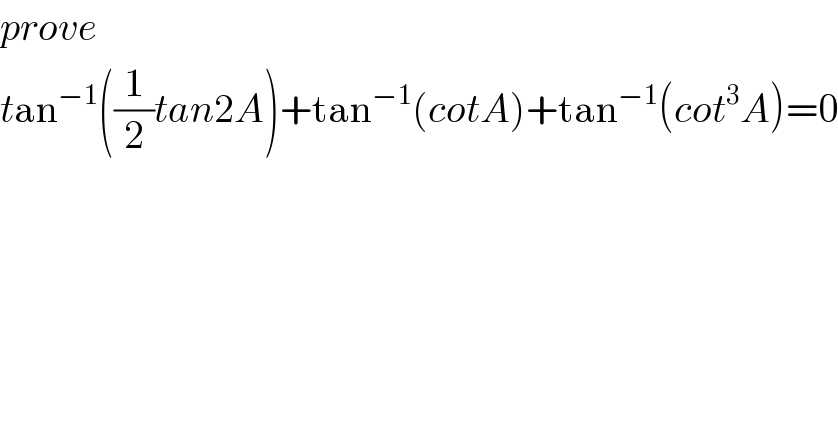
$${prove} \\ $$$${t}\mathrm{an}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}{tan}\mathrm{2}{A}\right)+\mathrm{tan}^{−\mathrm{1}} \left({cotA}\right)+\mathrm{tan}^{−\mathrm{1}} \left({cot}^{\mathrm{3}} {A}\right)=\mathrm{0} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 07/May/18

$${let}\:{tanA}={t} \\ $$$${tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} \:}\right)+{tan}^{−\mathrm{1}} \:\left(\frac{\mathrm{1}}{{t}}\right)+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{t}^{\mathrm{3}} }\right) \\ $$$$={tan}^{−\mathrm{1}} \left(\frac{\frac{{t}}{\mathrm{1}−{t}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{{t}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}−{t}^{\mathrm{2}\:_{} \:} \:}}\right)+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{t}^{\mathrm{3}} }\right) \\ $$$$={tan}^{−\mathrm{1}} \left(\frac{\frac{\mathrm{1}}{{t}−{t}^{\mathrm{3}} }}{\frac{\mathrm{1}−{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}−{t}^{\mathrm{2}} }}\right)+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{t}^{\mathrm{3}\:} }\right) \\ $$$${tan}^{−\mathrm{1}} \left\{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{{t}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left(−{t}^{\mathrm{2}} \right)}\right\}+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{t}^{\mathrm{3}\:} }\right) \\ $$$$={tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{−{t}^{\mathrm{3}} }\right)+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{t}^{\mathrm{3}} }\right\} \\ $$$$=−{tan}\left(\frac{\mathrm{1}}{{t}^{} }\right)+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{t}^{\mathrm{3}} }\:\right)=\mathrm{0} \\ $$
