Question Number 154208 by amin96 last updated on 15/Sep/21
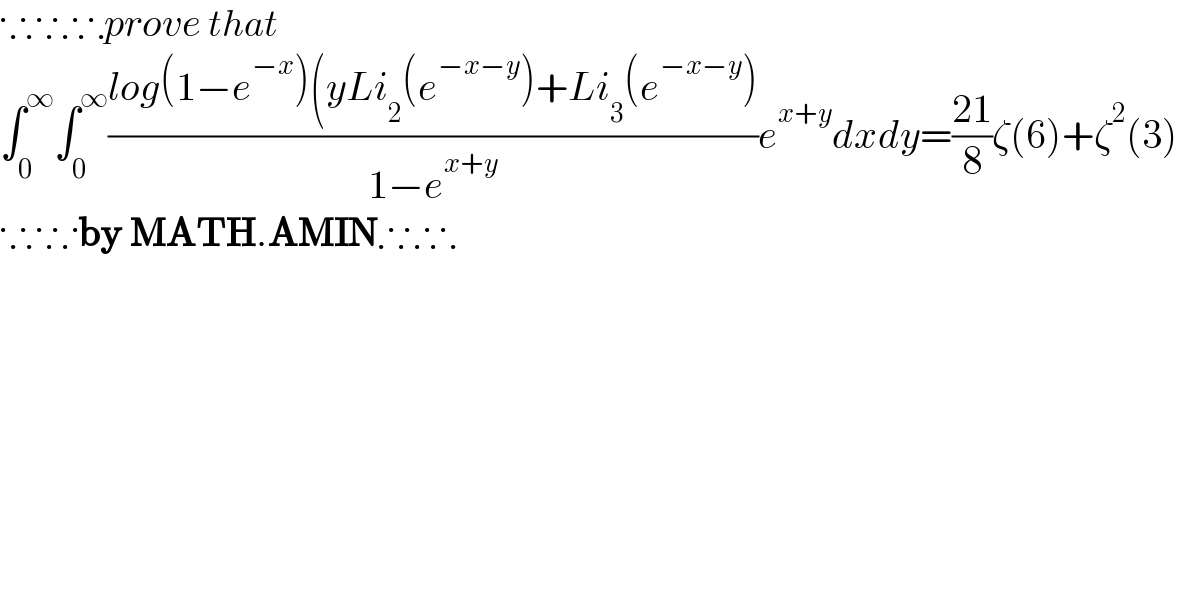
$$\because\therefore\because\therefore{prove}\:{that} \\ $$$$\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} \frac{{log}\left(\mathrm{1}−{e}^{−{x}} \right)\left({yLi}_{\mathrm{2}} \left({e}^{−{x}−{y}} \right)+{Li}_{\mathrm{3}} \left({e}^{−{x}−{y}} \right)\right.}{\mathrm{1}−{e}^{{x}+{y}} }{e}^{{x}+{y}} {dxdy}=\frac{\mathrm{21}}{\mathrm{8}}\zeta\left(\mathrm{6}\right)+\zeta^{\mathrm{2}} \left(\mathrm{3}\right) \\ $$$$\because\therefore\because\boldsymbol{\mathrm{by}}\:\boldsymbol{\mathrm{MATH}}.\boldsymbol{\mathrm{AMIN}}\therefore\because\therefore \\ $$
