Question Number 150226 by mnjuly1970 last updated on 10/Aug/21

$$ \\ $$$$\:\:\:\:\:\mathrm{prove}\:\:\mathrm{that}\::: \\ $$$$\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\zeta\:\left(\mathrm{0}\:\right)\overset{?} {=}\:\frac{−\mathrm{1}}{\mathrm{2}}\:……….\blacksquare \\ $$$$\:\:\:\:\:\:\:{m}.{n}… \\ $$
Answered by Kamel last updated on 10/Aug/21

$${By}\:{using}\:{fonctionnal}\:{relation}\:{of}\:{zeta}. \\ $$
Commented by mnjuly1970 last updated on 10/Aug/21

$$\:\:{yes}\:{mr}\:{kamel}….{mercey}… \\ $$
Answered by Kamel last updated on 10/Aug/21
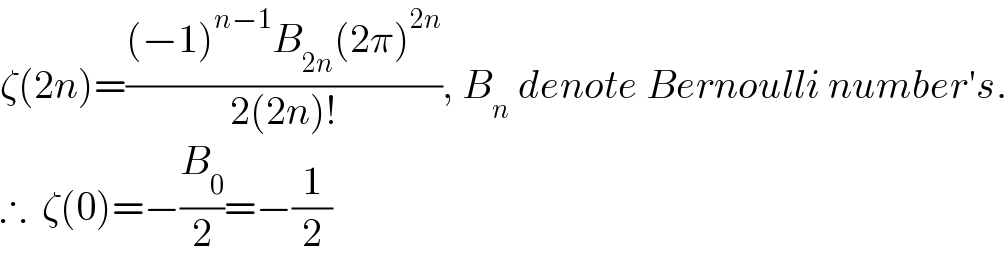
$$\zeta\left(\mathrm{2}{n}\right)=\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {B}_{\mathrm{2}{n}} \left(\mathrm{2}\pi\right)^{\mathrm{2}{n}} }{\mathrm{2}\left(\mathrm{2}{n}\right)!},\:{B}_{{n}} \:{denote}\:{Bernoulli}\:{number}'{s}. \\ $$$$\therefore\:\:\zeta\left(\mathrm{0}\right)=−\frac{{B}_{\mathrm{0}} }{\mathrm{2}}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
