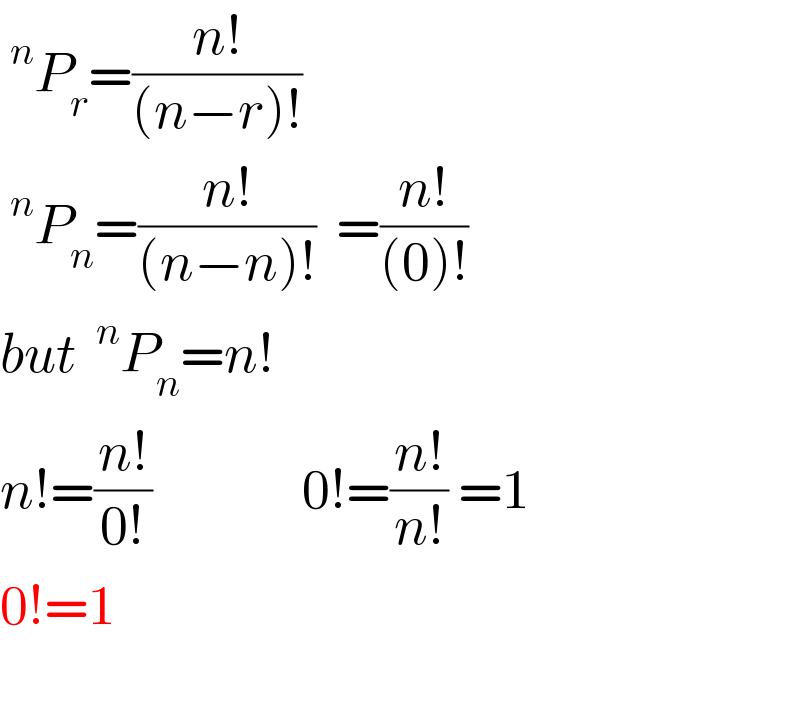prove-that-0-1-

Question Number 192112 by Spillover last updated on 08/May/23

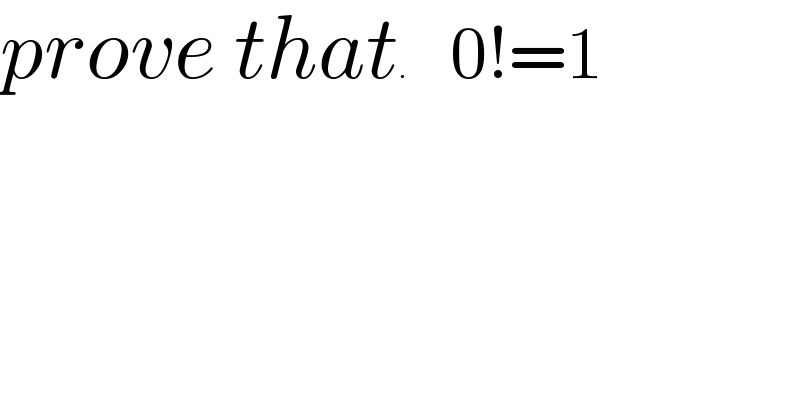
p r o v e t h a t . 0! = 1

Commented by Frix last updated on 08/May/23

I think {it}^{'} s defined 0! = 1

{There}^{'} s the idea of the “ Empty {Product}^{″}

{It}^{'} s obvious that the “ Empty {Sum}^{″} = 0

because if we sum up nothing we still

have nothing . Because the sum

\log x + \log y = \log x y we set the “ Empty

{Product}^{″} = 1

x! = \underset{k = 1}{\prod^{x}} \Rightarrow 0! is the “ Empty {Product}^{″}

But we can simply calculate backwards

3! = 6

2! = \frac{3!}{3} = 2

1! = \frac{2!}{2} = 1

0! = \frac{1!}{1} = 1

[\Rightarrow x! is not defined for x \in Z^{-}]

Commented by Spillover last updated on 12/May/23

t h a n k s

Answered by Skabetix last updated on 08/May/23

H e l l o

X! = X (X - 1)!

\Leftrightarrow (X - 1)! = \frac{X!}{X}

N o w w e j u s t h a v e t o t e s t f o r 0

(1 - 1)! = \frac{1!}{1}

\Leftrightarrow 0! = \frac{1}{1} = 1

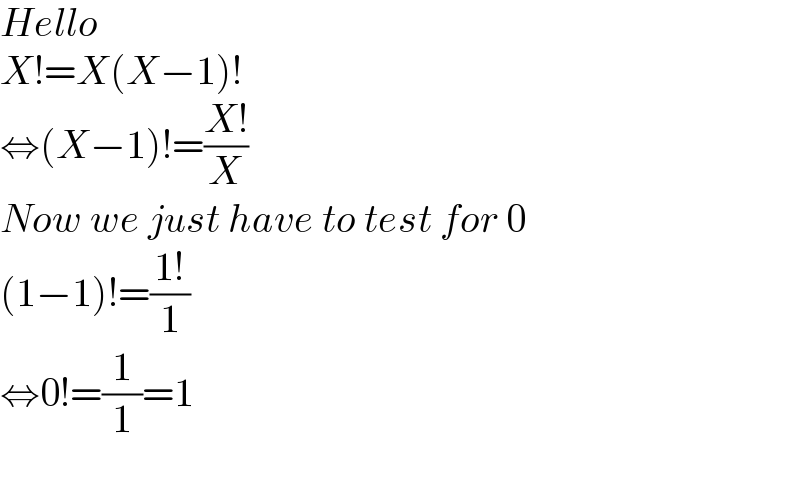
Answered by Spillover last updated on 12/May/23

^{n} P_{r} = \frac{n!}{(n - r)!}

^{n} P_{n} = \frac{n!}{(n - n)!} = \frac{n!}{(0)!}

b u t^{n} P_{n} = n!

n! = \frac{n!}{0!} 0! = \frac{n!}{n!} = 1

0! = 1