Question Number 63852 by aliesam last updated on 10/Jul/19
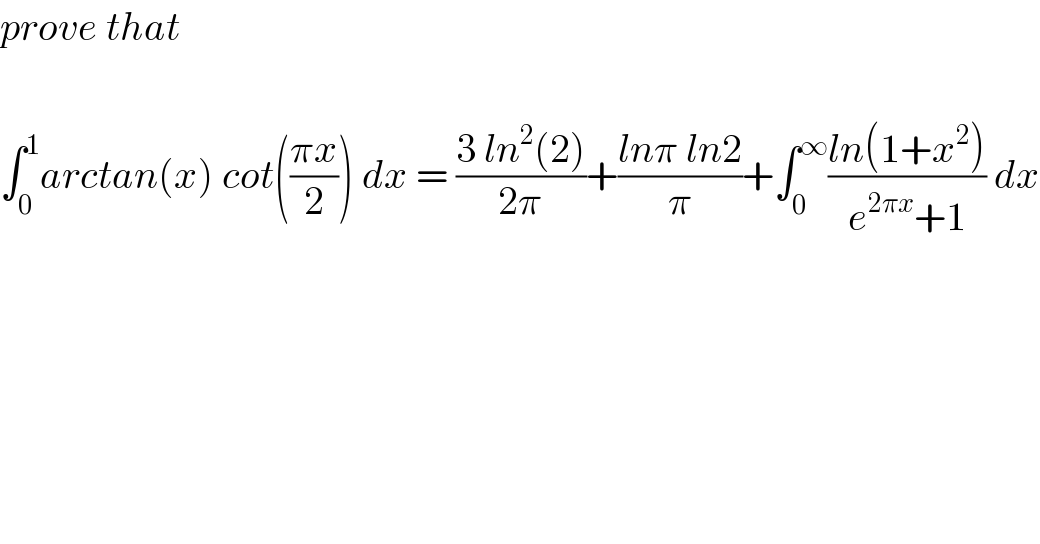
$${prove}\:{that} \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {arctan}\left({x}\right)\:{cot}\left(\frac{\pi{x}}{\mathrm{2}}\right)\:{dx}\:=\:\frac{\mathrm{3}\:{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}\pi}+\frac{{ln}\pi\:{ln}\mathrm{2}}{\pi}+\int_{\mathrm{0}} ^{\infty} \frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{{e}^{\mathrm{2}\pi{x}} +\mathrm{1}}\:{dx} \\ $$
