Question Number 43545 by peter frank last updated on 11/Sep/18
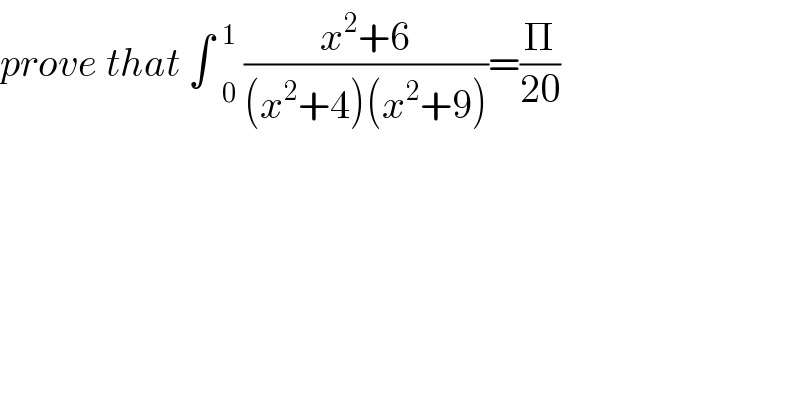
$${prove}\:{that}\:\int\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\:}}\:\frac{{x}^{\mathrm{2}} +\mathrm{6}}{\left({x}^{\mathrm{2}} +\mathrm{4}\right)\left({x}^{\mathrm{2}} +\mathrm{9}\right)}=\frac{\Pi}{\mathrm{20}} \\ $$
Answered by behi83417@gmail.com last updated on 12/Sep/18
![I=(1/2)∫((2x^2 +12)/((x^2 +4)(x^2 +9)))dx= =(1/2)[∫((1/(x^2 +9))+(1/(x^2 +4))−(1/5)((1/(x^2 +4))−(1/(x^2 +9)))]dx= =(3/5)∫ (dx/(x^2 +9))+(2/5)∫ (dx/(x^2 +4))= =(3/5).(1/3)tg^(−1) ((x/3))+(2/5).(1/2)tg^(−1) ((x/2))+c= =(1/5)tg^(−1) (((x/3)+(x/2))/(1−(x^2 /6)))=(1/5)tg^(−1) ((5x)/(6−x^2 ))+c. I=F(1)−F(0)=(1/5)[tg^(−1) (5/5)−0]= =(1/5).(π/4)=(π/(20)). ■](https://www.tinkutara.com/question/Q43553.png)
$${I}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{12}}{\left({x}^{\mathrm{2}} +\mathrm{4}\right)\left({x}^{\mathrm{2}} +\mathrm{9}\right)}{dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\int\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{9}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{5}}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{4}}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{9}}\right)\right]{dx}=\right. \\ $$$$=\frac{\mathrm{3}}{\mathrm{5}}\int\:\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{9}}+\frac{\mathrm{2}}{\mathrm{5}}\int\:\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{4}}= \\ $$$$=\frac{\mathrm{3}}{\mathrm{5}}.\frac{\mathrm{1}}{\mathrm{3}}{tg}^{−\mathrm{1}} \left(\frac{{x}}{\mathrm{3}}\right)+\frac{\mathrm{2}}{\mathrm{5}}.\frac{\mathrm{1}}{\mathrm{2}}{tg}^{−\mathrm{1}} \left(\frac{{x}}{\mathrm{2}}\right)+{c}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}{tg}^{−\mathrm{1}} \frac{\frac{{x}}{\mathrm{3}}+\frac{{x}}{\mathrm{2}}}{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}}=\frac{\mathrm{1}}{\mathrm{5}}{tg}^{−\mathrm{1}} \frac{\mathrm{5}{x}}{\mathrm{6}−{x}^{\mathrm{2}} }+{c}. \\ $$$${I}={F}\left(\mathrm{1}\right)−{F}\left(\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{5}}\left[{tg}^{−\mathrm{1}} \frac{\mathrm{5}}{\mathrm{5}}−\mathrm{0}\right]= \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}.\frac{\pi}{\mathrm{4}}=\frac{\pi}{\mathrm{20}}.\:\blacksquare \\ $$
