Question Number 88177 by M±th+et£s last updated on 08/Apr/20
![prove that ∫_0 ^(2020) (x−[x])(√(x−[x])) dx=808](https://www.tinkutara.com/question/Q88177.png)
$${prove}\:{that} \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2020}} \left({x}−\left[{x}\right]\right)\sqrt{{x}−\left[{x}\right]}\:{dx}=\mathrm{808} \\ $$
Answered by TANMAY PANACEA. last updated on 08/Apr/20
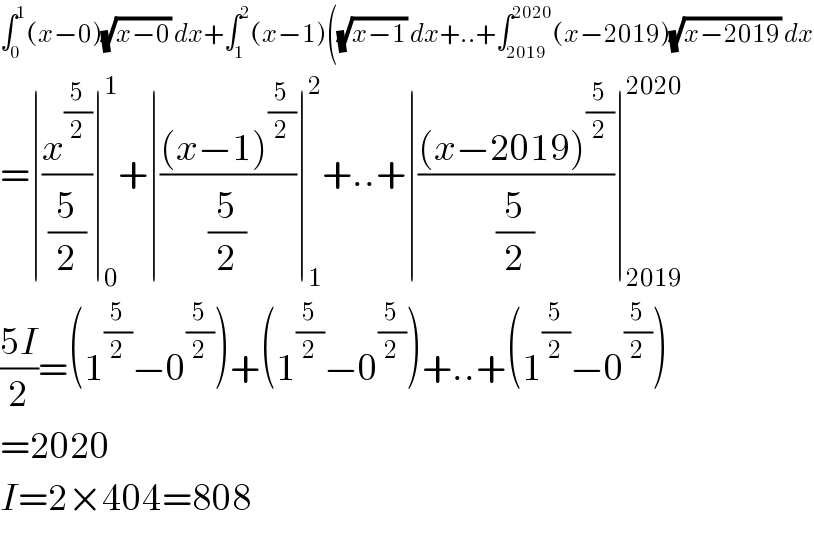
$$\int_{\mathrm{0}} ^{\mathrm{1}} \left({x}−\mathrm{0}\right)\sqrt{{x}−\mathrm{0}}\:{dx}+\int_{\mathrm{1}} ^{\mathrm{2}} \left({x}−\mathrm{1}\right)\left(\sqrt{{x}−\mathrm{1}}\:{dx}+..+\int_{\mathrm{2019}} ^{\mathrm{2020}} \left({x}−\mathrm{2019}\right)\sqrt{{x}−\mathrm{2019}}\:{dx}\right. \\ $$$$=\mid\frac{{x}^{\frac{\mathrm{5}}{\mathrm{2}}} }{\frac{\mathrm{5}}{\mathrm{2}}}\mid_{\mathrm{0}} ^{\mathrm{1}} +\mid\frac{\left({x}−\mathrm{1}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} }{\frac{\mathrm{5}}{\mathrm{2}}}\mid_{\mathrm{1}} ^{\mathrm{2}} +..+\mid\frac{\left({x}−\mathrm{2019}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} }{\frac{\mathrm{5}}{\mathrm{2}}}\mid_{\mathrm{2019}} ^{\mathrm{2020}} \\ $$$$\frac{\mathrm{5}{I}}{\mathrm{2}}=\left(\mathrm{1}^{\frac{\mathrm{5}}{\mathrm{2}}} −\mathrm{0}^{\frac{\mathrm{5}}{\mathrm{2}}} \right)+\left(\mathrm{1}^{\frac{\mathrm{5}}{\mathrm{2}}} −\mathrm{0}^{\frac{\mathrm{5}}{\mathrm{2}}} \right)+..+\left(\mathrm{1}^{\frac{\mathrm{5}}{\mathrm{2}}} −\mathrm{0}^{\frac{\mathrm{5}}{\mathrm{2}}} \right) \\ $$$$=\mathrm{2020} \\ $$$${I}=\mathrm{2}×\mathrm{404}=\mathrm{808} \\ $$
Commented by M±th+et£s last updated on 08/Apr/20

$${god}\:{bless}\:{you}\:{sir} \\ $$
Commented by TANMAY PANACEA. last updated on 08/Apr/20

$${most}\:{welcome}\:{sir}… \\ $$
