Question Number 123598 by aurpeyz last updated on 26/Nov/20
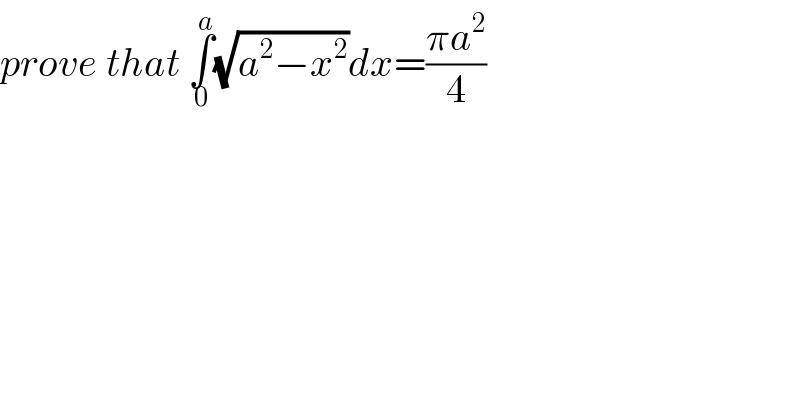
$${prove}\:{that}\:\underset{\mathrm{0}} {\overset{{a}} {\int}}\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }{dx}=\frac{\pi{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$
Answered by Dwaipayan Shikari last updated on 26/Nov/20
![∫_0 ^a (√(a^2 −x^2 )) dx x=asinθ ∫_0 ^(π/2) acosθ(√(a^2 −a^2 sin^2 θ)) dθ =a^2 ∫_0 ^(π/2) cos^2 θ =(a^2 /2)∫_0 ^(π/2) 1+cos2θ dx =((πa^2 )/4)+(a^2 /2)∫_0 ^(π/2) cos2θ =((πa^2 )/4)+(a^2 /4)[cos2θ]_0 ^(π/2) =((πa^2 )/4)](https://www.tinkutara.com/question/Q123602.png)
$$\int_{\mathrm{0}} ^{{a}} \sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\:{dx}\:\:\:\:\:\:\:\:{x}={asin}\theta \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {acos}\theta\sqrt{{a}^{\mathrm{2}} −{a}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}\:{d}\theta \\ $$$$={a}^{\mathrm{2}} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{2}} \theta\:=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{1}+{cos}\mathrm{2}\theta\:{dx} \\ $$$$=\frac{\pi{a}^{\mathrm{2}} }{\mathrm{4}}+\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}\mathrm{2}\theta\:=\frac{\pi{a}^{\mathrm{2}} }{\mathrm{4}}+\frac{{a}^{\mathrm{2}} }{\mathrm{4}}\left[{cos}\mathrm{2}\theta\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\frac{\pi{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$
