Question Number 124888 by mnjuly1970 last updated on 06/Dec/20
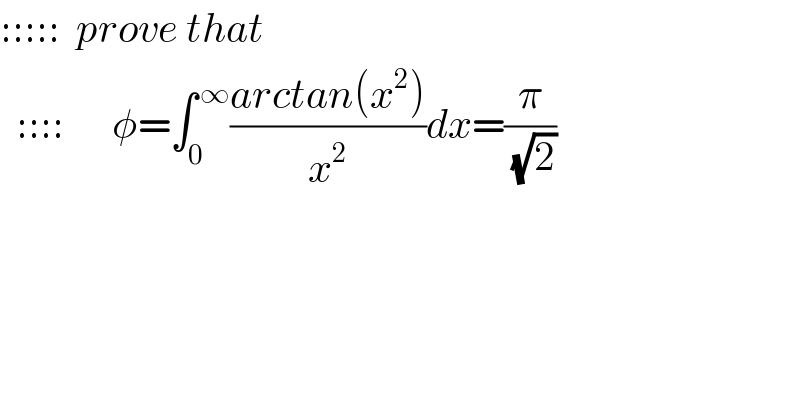
$$:::::\:\:{prove}\:{that}\: \\ $$$$\:\:::::\:\:\:\:\:\:\phi=\int_{\mathrm{0}} ^{\:\infty} \frac{{arctan}\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }{dx}=\frac{\pi}{\:\sqrt{\mathrm{2}}} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$
Answered by mnjuly1970 last updated on 06/Dec/20
![solution φ=^(x=(1/t)⇒) ∫_0 ^( ∞) arccot(t^2 )dt=[tarccot(t^2 )]_0 ^∞ +2∫_0 ^( ∞) (t^2 /(1+t^4 ))dt =^(t^4 =u) (1/2)∫_0 ^( ∞) ((u^(1/2) u^((−3)/4) )/(1+u))du=(1/2)Γ((3/4))Γ((1/4)) =(1/2) (π/(sin((π/4))))=(1/2) ((2π)/( (√2)))=(π/( (√2))) ✓](https://www.tinkutara.com/question/Q124896.png)
$${solution} \\ $$$$\:\phi\overset{{x}=\frac{\mathrm{1}}{{t}}\Rightarrow} {=}\int_{\mathrm{0}} ^{\:\infty} {arccot}\left({t}^{\mathrm{2}} \right){dt}=\left[{tarccot}\left({t}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\infty} +\mathrm{2}\int_{\mathrm{0}} ^{\:\infty} \frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{4}} }{dt} \\ $$$$\overset{{t}^{\mathrm{4}} ={u}} {=}\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\infty} \frac{{u}^{\frac{\mathrm{1}}{\mathrm{2}}} {u}^{\frac{−\mathrm{3}}{\mathrm{4}}} }{\mathrm{1}+{u}}{du}=\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{4}}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{2}}}=\frac{\pi}{\:\sqrt{\mathrm{2}}}\:\checkmark \\ $$
Commented by Dwaipayan Shikari last updated on 06/Dec/20

$${Great}\:{sir}! \\ $$
Commented by mnjuly1970 last updated on 06/Dec/20

$${thanks}\:{alot}.. \\ $$
Answered by Dwaipayan Shikari last updated on 06/Dec/20
![∫_0 ^∞ ((tan^(−1) (x^2 ))/x^2 )dx =[ −((tan^(−1) x^2 )/x)]_0 ^∞ +∫_0 ^∞ ((2x)/(x(x^4 +1)))dx =2∫_0 ^∞ (dx/((x^4 +1)))=∫_0 ^(π/2) (dθ/( (√(tanθ))(tan^2 θ+1)))sec^2 θ x^2 =tanθ =2∫_0 ^(π/2) (1/( (√(tanθ))))dθ=2∫_0 ^(π/2) (1/( (√(cotθ))))dθ=I ⇒2I=2∫_0 ^(π/2) ((sinθ+cosθ)/( (√(sinθcosθ))))dθ ⇒I=(√2)∫_0 ^(π/2) ((sinθ+cosθ)/( (√(1−(sinθ−cosθ)^2 ))))dθ=(√2)∫_0 ^1 (dt/( (√(1−t^2 )))) ⇒I=(√2)[sin^(−1) t]_0 ^1 =(π/( (√2)))](https://www.tinkutara.com/question/Q124889.png)
$$\int_{\mathrm{0}} ^{\infty} \frac{{tan}^{−\mathrm{1}} \left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }{dx}\:=\left[\:−\frac{{tan}^{−\mathrm{1}} {x}^{\mathrm{2}} }{{x}}\right]_{\mathrm{0}} ^{\infty} +\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}{x}}{{x}\left({x}^{\mathrm{4}} +\mathrm{1}\right)}{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\left({x}^{\mathrm{4}} +\mathrm{1}\right)}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{d}\theta}{\:\sqrt{{tan}\theta}\left({tan}^{\mathrm{2}} \theta+\mathrm{1}\right)}{sec}^{\mathrm{2}} \theta\:\:\:\:\:\:\:{x}^{\mathrm{2}} ={tan}\theta \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\:\sqrt{{tan}\theta}}{d}\theta=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\:\sqrt{{cot}\theta}}{d}\theta={I} \\ $$$$\Rightarrow\mathrm{2}{I}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}\theta+{cos}\theta}{\:\sqrt{{sin}\theta{cos}\theta}}{d}\theta \\ $$$$\Rightarrow{I}=\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}\theta+{cos}\theta}{\:\sqrt{\mathrm{1}−\left({sin}\theta−{cos}\theta\right)^{\mathrm{2}} }}{d}\theta=\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }} \\ $$$$\Rightarrow{I}=\sqrt{\mathrm{2}}\left[{sin}^{−\mathrm{1}} {t}\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\pi}{\:\sqrt{\mathrm{2}}} \\ $$
Commented by mnjuly1970 last updated on 06/Dec/20

$${thank}\:{you}\:{mr} \\ $$$${dwaipayan}.. \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 06/Dec/20
![I =∫_0 ^∞ ((arctan(x^2 ))/x^2 )dx by psrts I=[−(1/x)arctan(x^2 )]_0 ^∞ +∫_0 ^∞ (1/x)×((2x)/(1+x^4 ))dx =2∫_0 ^∞ (dx/(1+x^4 )) =_(x=t^(1/4) ) 2 ∫_0 ^∞ (1/(4(1+t)))t^((1/4)−1) dt =(1/2)∫_0 ^∞ (t^((1/4)−1) /(1+t))dt =(1/2)×(π/(sin((π/4))))=(π/(2×(1/( (√2))))) =(π/( (√2))) ⇒I =(π/( (√2)))](https://www.tinkutara.com/question/Q124912.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{arctan}\left(\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\mathrm{by}\:\mathrm{psrts}\:\:\mathrm{I}=\left[−\frac{\mathrm{1}}{\mathrm{x}}\mathrm{arctan}\left(\mathrm{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\infty} +\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{x}}×\frac{\mathrm{2x}}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\:=_{\mathrm{x}=\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{4}}} } \:\:\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{1}+\mathrm{t}\right)}\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} \mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi}{\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}\right)}=\frac{\pi}{\mathrm{2}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}\:=\frac{\pi}{\:\sqrt{\mathrm{2}}}\:\Rightarrow\mathrm{I}\:=\frac{\pi}{\:\sqrt{\mathrm{2}}} \\ $$
