Question Number 113004 by malwan last updated on 10/Sep/20

$${prove}\:{that} \\ $$$$\:_{\mathrm{0}} \int^{\:\infty} \:{cos}\left({x}^{\mathrm{2}} \right){dx}\:=\:\:_{\mathrm{0}} \int^{\:\infty} {sin}\left({x}^{\mathrm{2}} \right){dx}\:=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$
Answered by mathdave last updated on 10/Sep/20
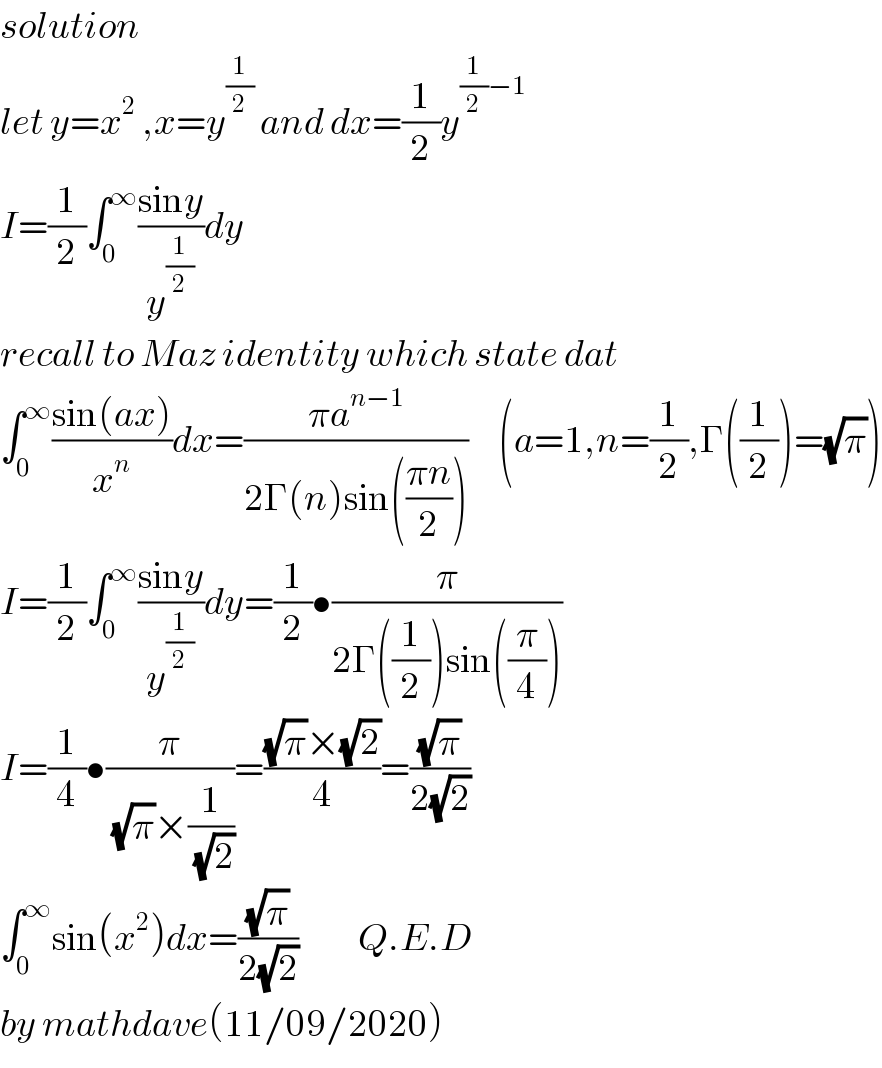
$${solution}\: \\ $$$${let}\:{y}={x}^{\mathrm{2}} \:,{x}={y}^{\frac{\mathrm{1}}{\mathrm{2}}} \:{and}\:{dx}=\frac{\mathrm{1}}{\mathrm{2}}{y}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{y}}{{y}^{\frac{\mathrm{1}}{\mathrm{2}}} }{dy} \\ $$$${recall}\:{to}\:{Maz}\:{identity}\:{which}\:{state}\:{dat} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}\left({ax}\right)}{{x}^{{n}} }{dx}=\frac{\pi{a}^{{n}−\mathrm{1}} }{\mathrm{2}\Gamma\left({n}\right)\mathrm{sin}\left(\frac{\pi{n}}{\mathrm{2}}\right)}\:\:\:\:\:\left({a}=\mathrm{1},{n}=\frac{\mathrm{1}}{\mathrm{2}},\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\sqrt{\pi}\right) \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{y}}{{y}^{\frac{\mathrm{1}}{\mathrm{2}}} }{dy}=\frac{\mathrm{1}}{\mathrm{2}}\bullet\frac{\pi}{\mathrm{2}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}\right)} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{4}}\bullet\frac{\pi}{\:\sqrt{\pi}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}=\frac{\sqrt{\pi}×\sqrt{\mathrm{2}}}{\mathrm{4}}=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \mathrm{sin}\left({x}^{\mathrm{2}} \right){dx}=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\:\:\:\:\:\:\:\:\:{Q}.{E}.{D} \\ $$$${by}\:{mathdave}\left(\mathrm{11}/\mathrm{09}/\mathrm{2020}\right) \\ $$
Commented by malwan last updated on 11/Sep/20
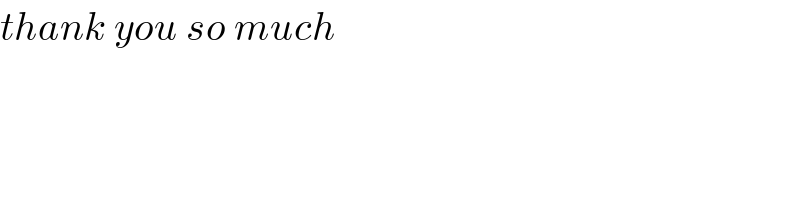
$${thank}\:{you}\:{so}\:{much} \\ $$
Commented by Tawa11 last updated on 06/Sep/21

$$\mathrm{great}\:\mathrm{sir} \\ $$
Answered by mathmax by abdo last updated on 10/Sep/20
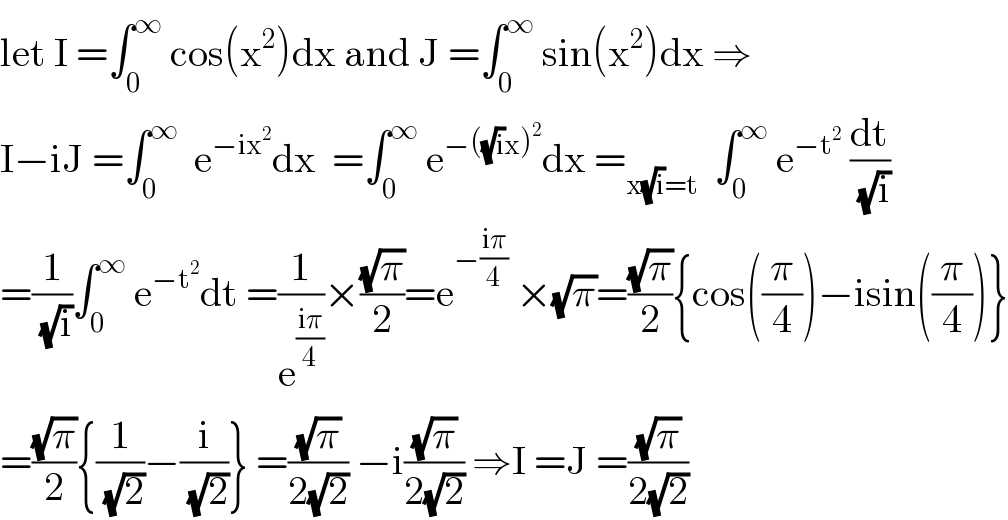
$$\mathrm{let}\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{cos}\left(\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx}\:\mathrm{and}\:\mathrm{J}\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{sin}\left(\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{I}−\mathrm{iJ}\:=\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\mathrm{ix}^{\mathrm{2}} } \mathrm{dx}\:\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\sqrt{\mathrm{i}}\mathrm{x}\right)^{\mathrm{2}} } \mathrm{dx}\:=_{\mathrm{x}\sqrt{\mathrm{i}}=\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \:\frac{\mathrm{dt}}{\:\sqrt{\mathrm{i}}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{i}}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} }×\frac{\sqrt{\pi}}{\mathrm{2}}=\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \:×\sqrt{\pi}=\frac{\sqrt{\pi}}{\mathrm{2}}\left\{\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}\right)−\mathrm{isin}\left(\frac{\pi}{\mathrm{4}}\right)\right\} \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{2}}\left\{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{i}}{\:\sqrt{\mathrm{2}}}\right\}\:=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{2}}}\:−\mathrm{i}\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\Rightarrow\mathrm{I}\:=\mathrm{J}\:=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$
Commented by malwan last updated on 11/Sep/20

$${great}\:{Sir} \\ $$$${thank}\:{you} \\ $$
