Question Number 152494 by mnjuly1970 last updated on 28/Aug/21
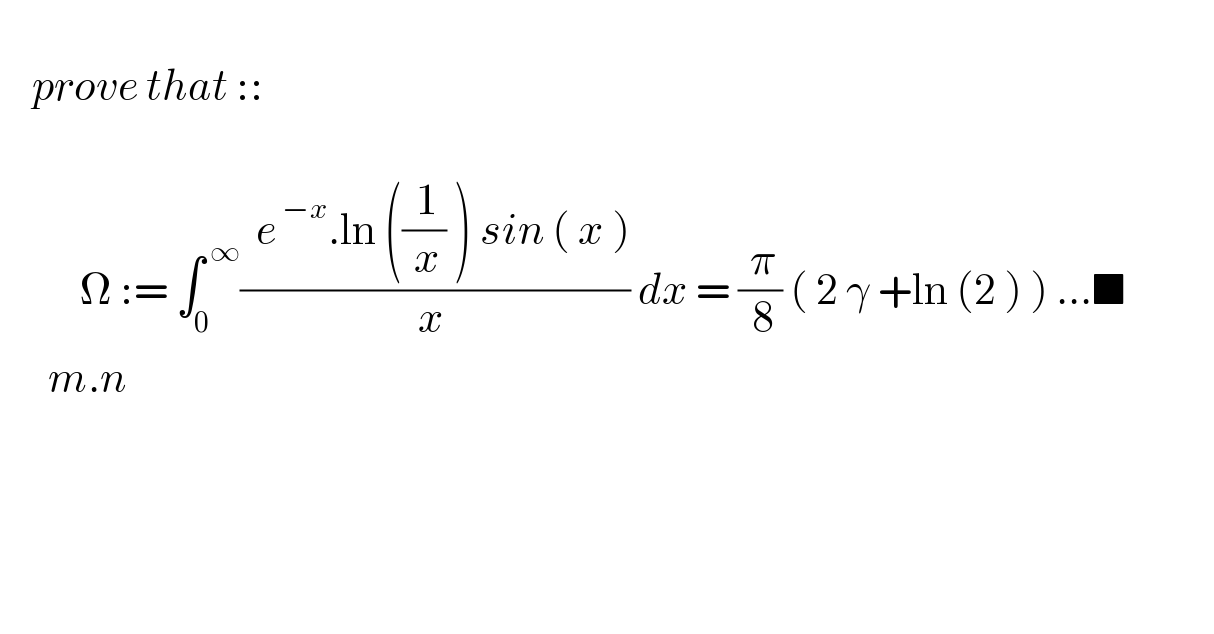
$$ \\ $$$$\:\:\:\:{prove}\:{that}\::: \\ $$$$\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\Omega\::=\:\int_{\mathrm{0}\:} ^{\:\infty} \frac{\:\:{e}^{\:−{x}} .\mathrm{ln}\:\left(\frac{\:\mathrm{1}}{\:{x}}\:\right)\:{sin}\:\left(\:{x}\:\right)}{{x}\:}\:{dx}\:=\:\frac{\:\pi}{\:\mathrm{8}}\:\left(\:\mathrm{2}\:\gamma\:+\mathrm{ln}\:\left(\mathrm{2}\:\right)\:\right)\:…\blacksquare\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:{m}.{n} \\ $$$$ \\ $$
Answered by Olaf_Thorendsen last updated on 31/Aug/21
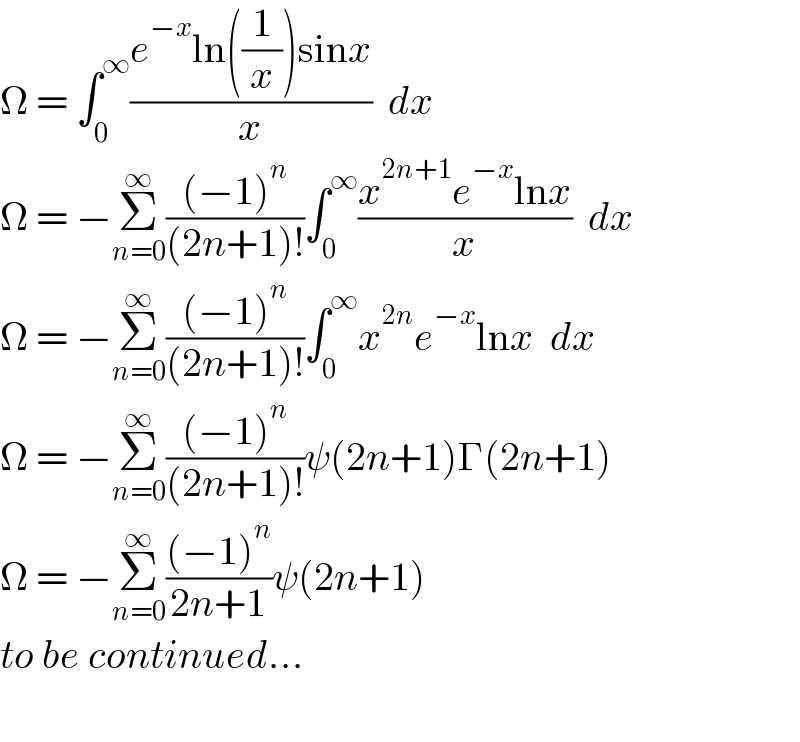
$$\Omega\:=\:\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}} \mathrm{ln}\left(\frac{\mathrm{1}}{{x}}\right)\mathrm{sin}{x}}{{x}}\:\:{dx} \\ $$$$\Omega\:=\:−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}{n}+\mathrm{1}} {e}^{−{x}} \mathrm{ln}{x}}{{x}}\:\:{dx} \\ $$$$\Omega\:=\:−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{2}{n}} {e}^{−{x}} \mathrm{ln}{x}\:\:{dx} \\ $$$$\Omega\:=\:−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\psi\left(\mathrm{2}{n}+\mathrm{1}\right)\Gamma\left(\mathrm{2}{n}+\mathrm{1}\right) \\ $$$$\Omega\:=\:−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\psi\left(\mathrm{2}{n}+\mathrm{1}\right) \\ $$$${to}\:{be}\:{continued}… \\ $$$$ \\ $$
