Menu Close

Prove-that-0-sh-t-sh-t-dt-2-tan-2-

Tinku Tara 0 Comments
Pin




Question Number 144180 by Willson last updated on 22/Jun/21
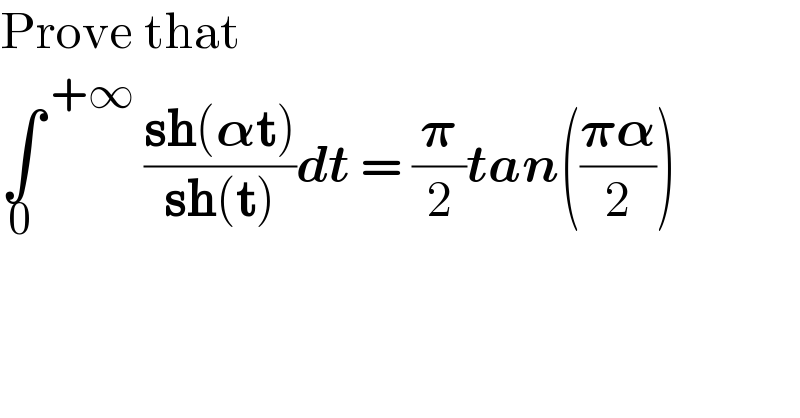
Prove that ∫^( +∞) _0 ((sh(𝛂t))/(sh(t)))dt = (𝛑/2)tan(((𝛑𝛂)/2))
$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\underset{\mathrm{0}} {\int}^{\:+\infty} \:\frac{\boldsymbol{\mathrm{sh}}\left(\boldsymbol{\alpha\mathrm{t}}\right)}{\boldsymbol{\mathrm{sh}}\left(\boldsymbol{\mathrm{t}}\right)}\boldsymbol{{dt}}\:=\:\frac{\boldsymbol{\pi}}{\mathrm{2}}\boldsymbol{{tan}}\left(\frac{\boldsymbol{\pi\alpha}}{\mathrm{2}}\right) \\ $$
Answered by mindispower last updated on 22/Jun/21
=∫_0 ^∞ ((e^(at) βˆ’e^(βˆ’at) )/(e^t βˆ’e^(βˆ’t) ))dt= e^(βˆ’t) =u β‡”βˆ«_0 ^1 ((u^(βˆ’a) βˆ’u^a )/((1/u)βˆ’u)).(1/u)du =∫_0 ^1 ((u^(βˆ’a) βˆ’u^a )/(1βˆ’u^2 ))du =∫_0 ^1 ((x^((βˆ’a)/2) βˆ’x^(a/2) )/(1βˆ’x)).(x^(βˆ’(1/2)) /2) =(1/2)∫_0 ^1 ((x^(βˆ’((a+1)/2)) βˆ’x^((aβˆ’1)/2) )/(1βˆ’x))dx Ξ¨(x+1)=βˆ’Ξ³+∫_0 ^1 ((1βˆ’t^x )/(1βˆ’t))dt we get(1/2)( Ξ¨(((a+1)/2))βˆ’Ξ¨(((1βˆ’a)/2)))=(1/2)(Ξ¨(1βˆ’((1βˆ’a)/2))βˆ’Ξ¨(((1βˆ’a)/2))) Ξ¨(1βˆ’z)βˆ’Ξ¨(z)=Ο€cot(Ο€z) we get (1/2)(Ο€cot(((Ο€(1βˆ’a))/2)))=(Ο€/2)cot((Ο€/2)βˆ’((aΟ€)/2)) =(Ο€/2)tan(((aΟ€)/2))
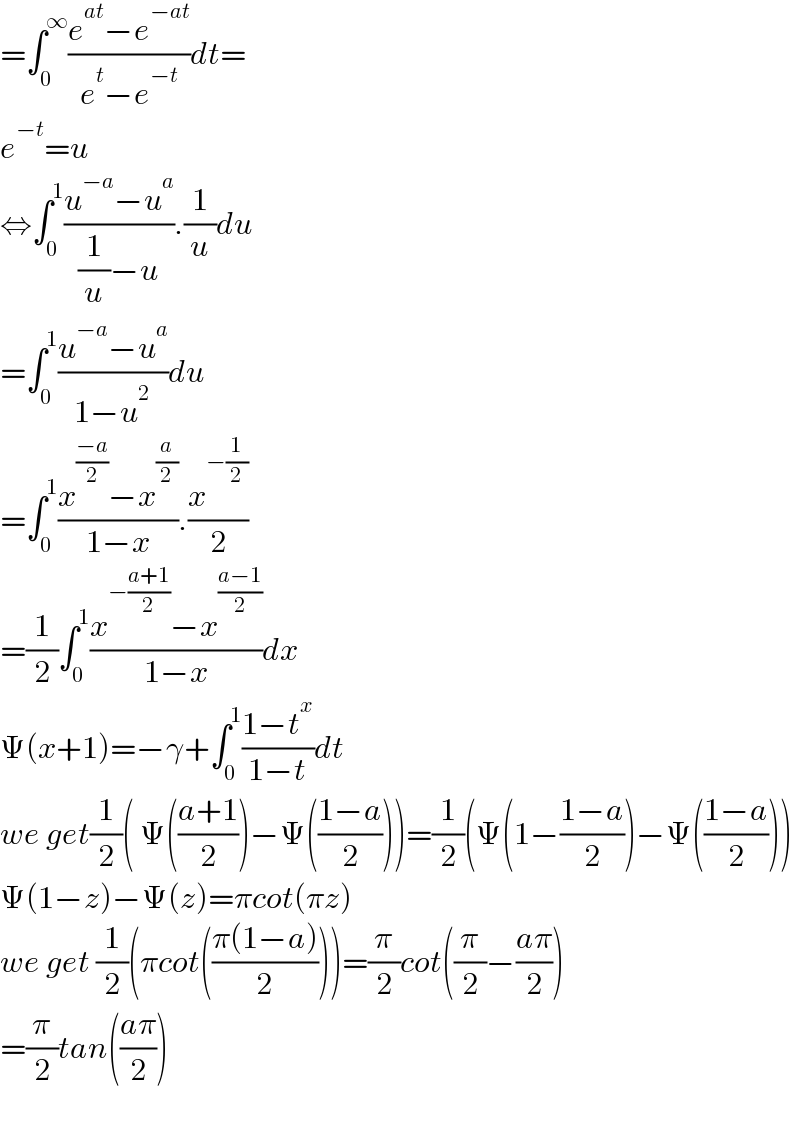
$$=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{{at}} βˆ’{e}^{βˆ’{at}} }{{e}^{{t}} βˆ’{e}^{βˆ’{t}} }{dt}= \\ $$$${e}^{βˆ’{t}} ={u} \\ $$$$\Leftrightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{βˆ’{a}} βˆ’{u}^{{a}} }{\frac{\mathrm{1}}{{u}}βˆ’{u}}.\frac{\mathrm{1}}{{u}}{du} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{βˆ’{a}} βˆ’{u}^{{a}} }{\mathrm{1}βˆ’{u}^{\mathrm{2}} }{du} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\frac{βˆ’{a}}{\mathrm{2}}} βˆ’{x}^{\frac{{a}}{\mathrm{2}}} }{\mathrm{1}βˆ’{x}}.\frac{{x}^{βˆ’\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{βˆ’\frac{{a}+\mathrm{1}}{\mathrm{2}}} βˆ’{x}^{\frac{{a}βˆ’\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}βˆ’{x}}{dx} \\ $$$$\Psi\left({x}+\mathrm{1}\right)=βˆ’\gamma+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}βˆ’{t}^{{x}} }{\mathrm{1}βˆ’{t}}{dt} \\ $$$${we}\:{get}\frac{\mathrm{1}}{\mathrm{2}}\left(\:\Psi\left(\frac{{a}+\mathrm{1}}{\mathrm{2}}\right)βˆ’\Psi\left(\frac{\mathrm{1}βˆ’{a}}{\mathrm{2}}\right)\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\Psi\left(\mathrm{1}βˆ’\frac{\mathrm{1}βˆ’{a}}{\mathrm{2}}\right)βˆ’\Psi\left(\frac{\mathrm{1}βˆ’{a}}{\mathrm{2}}\right)\right) \\ $$$$\Psi\left(\mathrm{1}βˆ’{z}\right)βˆ’\Psi\left({z}\right)=\pi{cot}\left(\pi{z}\right) \\ $$$${we}\:{get}\:\frac{\mathrm{1}}{\mathrm{2}}\left(\pi{cot}\left(\frac{\pi\left(\mathrm{1}βˆ’{a}\right)}{\mathrm{2}}\right)\right)=\frac{\pi}{\mathrm{2}}{cot}\left(\frac{\pi}{\mathrm{2}}βˆ’\frac{{a}\pi}{\mathrm{2}}\right) \\ $$$$=\frac{\pi}{\mathrm{2}}{tan}\left(\frac{{a}\pi}{\mathrm{2}}\right) \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 23/Jun/21
Ξ¦=∫_0 ^∞ ((sh(Ξ±t))/(sh(t)))dt β‡’Ξ¦=∫_0 ^∞ ((e^(Ξ±t) βˆ’e^(βˆ’Ξ±t) )/(e^t βˆ’e^(βˆ’t) ))dt =_(e^(βˆ’t) =x) βˆ’βˆ«_0 ^1 ((x^(βˆ’Ξ±) βˆ’x^Ξ± )/(x^(βˆ’1) βˆ’x))(βˆ’(dx/x)) =∫_0 ^1 ((x^(βˆ’Ξ±) βˆ’x^Ξ± )/(1βˆ’x^2 ))dx =_(x^2 =y) ∫_0 ^1 ((y^(βˆ’(Ξ±/2)) βˆ’y^(Ξ±/2) )/(1βˆ’y))(dy/(2(√y))) =(1/2)∫_0 ^1 ((y^(βˆ’((Ξ±+1)/2)) βˆ’y^((Ξ±βˆ’1)/2) )/(1βˆ’y))dy =βˆ’(1/2)∫_0 ^1 ((1βˆ’y^(βˆ’((Ξ±+1)/2)) )/(1βˆ’y))dy +(1/2)∫_0 ^1 ((1βˆ’y^((Ξ±βˆ’1)/2) )/(1βˆ’y))dy we know Ξ¨(z+1)=βˆ’Ξ³ +∫_0 ^1 ((1βˆ’y^z )/(1βˆ’y))dy β‡’ ∫_0 ^1 ((1βˆ’y^(βˆ’((Ξ±+1)/2)) )/(1βˆ’y))dy=Ξ¨(1βˆ’((Ξ±+1)/2))+Ξ³=Ξ¨(((1βˆ’Ξ±)/2))+Ξ³ ∫_0 ^1 ((1βˆ’y^((Ξ±βˆ’1)/2) )/(1βˆ’y))dy =Ξ¨(1+((Ξ±βˆ’1)/2))+Ξ³=Ξ¨(((Ξ±+1)/2)) β‡’ Ξ¦=(1/2){Ξ¨(((Ξ±+1)/2))βˆ’Ξ¨(((1βˆ’Ξ±)/2))} we have also Ξ¨(1βˆ’z)βˆ’Ξ¨(z)=Ο€cotan(Ο€z) β‡’ Ξ¨(((1+Ξ±)/2))βˆ’Ξ¨(((1βˆ’Ξ±)/2))=Ξ¨(1βˆ’((1βˆ’Ξ±)/2))βˆ’Ξ¨(((1βˆ’Ξ±)/2)) =Ο€cotan(Ο€(((1βˆ’Ξ±)/2)))=Ο€cotan((Ο€/2)βˆ’((πα)/2))=Ο€tan(((πα)/2))
$$\Phi=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sh}\left(\alpha\mathrm{t}\right)}{\mathrm{sh}\left(\mathrm{t}\right)}\mathrm{dt}\:\Rightarrow\Phi=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{e}^{\alpha\mathrm{t}} βˆ’\mathrm{e}^{βˆ’\alpha\mathrm{t}} }{\mathrm{e}^{\mathrm{t}} βˆ’\mathrm{e}^{βˆ’\mathrm{t}} }\mathrm{dt} \\ $$$$=_{\mathrm{e}^{βˆ’\mathrm{t}} \:=\mathrm{x}} \:\:βˆ’\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{βˆ’\alpha} βˆ’\mathrm{x}^{\alpha} }{\mathrm{x}^{βˆ’\mathrm{1}} βˆ’\mathrm{x}}\left(βˆ’\frac{\mathrm{dx}}{\mathrm{x}}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{βˆ’\alpha} βˆ’\mathrm{x}^{\alpha} }{\mathrm{1}βˆ’\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=_{\mathrm{x}^{\mathrm{2}} \:=\mathrm{y}} \:\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{y}^{βˆ’\frac{\alpha}{\mathrm{2}}} βˆ’\mathrm{y}^{\frac{\alpha}{\mathrm{2}}} }{\mathrm{1}βˆ’\mathrm{y}}\frac{\mathrm{dy}}{\mathrm{2}\sqrt{\mathrm{y}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{y}^{βˆ’\frac{\alpha+\mathrm{1}}{\mathrm{2}}} βˆ’\mathrm{y}^{\frac{\alphaβˆ’\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}βˆ’\mathrm{y}}\mathrm{dy}\:\:=βˆ’\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}βˆ’\mathrm{y}^{βˆ’\frac{\alpha+\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}βˆ’\mathrm{y}}\mathrm{dy}\:+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}βˆ’\mathrm{y}^{\frac{\alphaβˆ’\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}βˆ’\mathrm{y}}\mathrm{dy} \\ $$$$\mathrm{we}\:\mathrm{know}\:\Psi\left(\mathrm{z}+\mathrm{1}\right)=βˆ’\gamma\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}βˆ’\mathrm{y}^{\mathrm{z}} }{\mathrm{1}βˆ’\mathrm{y}}\mathrm{dy}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}βˆ’\mathrm{y}^{βˆ’\frac{\alpha+\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}βˆ’\mathrm{y}}\mathrm{dy}=\Psi\left(\mathrm{1}βˆ’\frac{\alpha+\mathrm{1}}{\mathrm{2}}\right)+\gamma=\Psi\left(\frac{\mathrm{1}βˆ’\alpha}{\mathrm{2}}\right)+\gamma \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}βˆ’\mathrm{y}^{\frac{\alphaβˆ’\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}βˆ’\mathrm{y}}\mathrm{dy}\:=\Psi\left(\mathrm{1}+\frac{\alphaβˆ’\mathrm{1}}{\mathrm{2}}\right)+\gamma=\Psi\left(\frac{\alpha+\mathrm{1}}{\mathrm{2}}\right)\:\Rightarrow \\ $$$$\Phi=\frac{\mathrm{1}}{\mathrm{2}}\left\{\Psi\left(\frac{\alpha+\mathrm{1}}{\mathrm{2}}\right)βˆ’\Psi\left(\frac{\mathrm{1}βˆ’\alpha}{\mathrm{2}}\right)\right\} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{also}\:\Psi\left(\mathrm{1}βˆ’\mathrm{z}\right)βˆ’\Psi\left(\mathrm{z}\right)=\pi\mathrm{cotan}\left(\pi\mathrm{z}\right)\:\Rightarrow \\ $$$$\Psi\left(\frac{\mathrm{1}+\alpha}{\mathrm{2}}\right)βˆ’\Psi\left(\frac{\mathrm{1}βˆ’\alpha}{\mathrm{2}}\right)=\Psi\left(\mathrm{1}βˆ’\frac{\mathrm{1}βˆ’\alpha}{\mathrm{2}}\right)βˆ’\Psi\left(\frac{\mathrm{1}βˆ’\alpha}{\mathrm{2}}\right) \\ $$$$=\pi\mathrm{cotan}\left(\pi\left(\frac{\mathrm{1}βˆ’\alpha}{\mathrm{2}}\right)\right)=\pi\mathrm{cotan}\left(\frac{\pi}{\mathrm{2}}βˆ’\frac{\pi\alpha}{\mathrm{2}}\right)=\pi\mathrm{tan}\left(\frac{\pi\alpha}{\mathrm{2}}\right) \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *