Question Number 94123 by M±th+et+s last updated on 17/May/20
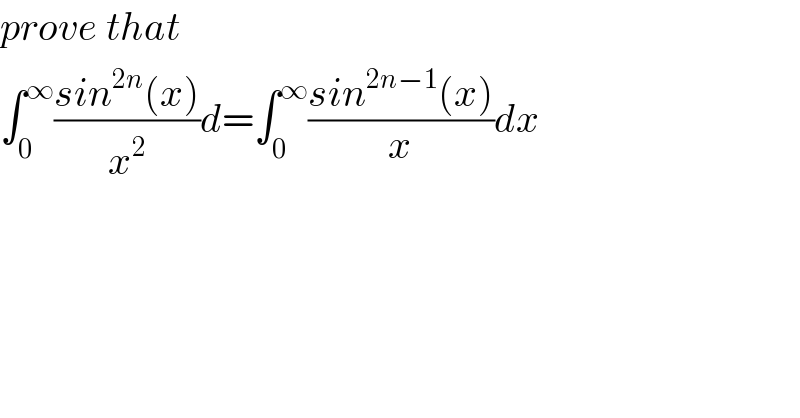
$${prove}\:{that} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{sin}^{\mathrm{2}{n}} \left({x}\right)}{{x}^{\mathrm{2}} }{d}=\int_{\mathrm{0}} ^{\infty} \frac{{sin}^{\mathrm{2}{n}−\mathrm{1}} \left({x}\right)}{{x}}{dx} \\ $$$$ \\ $$$$ \\ $$
