Menu Close

prove-that-0-sin-x-sin-pi-3-x-sin-2pi-3-x-ln-1-x-2-x-dx-pi-ln-3-m-n-

Tinku Tara 0 Comments
Pin




Question Number 159540 by mnjuly1970 last updated on 18/Nov/21
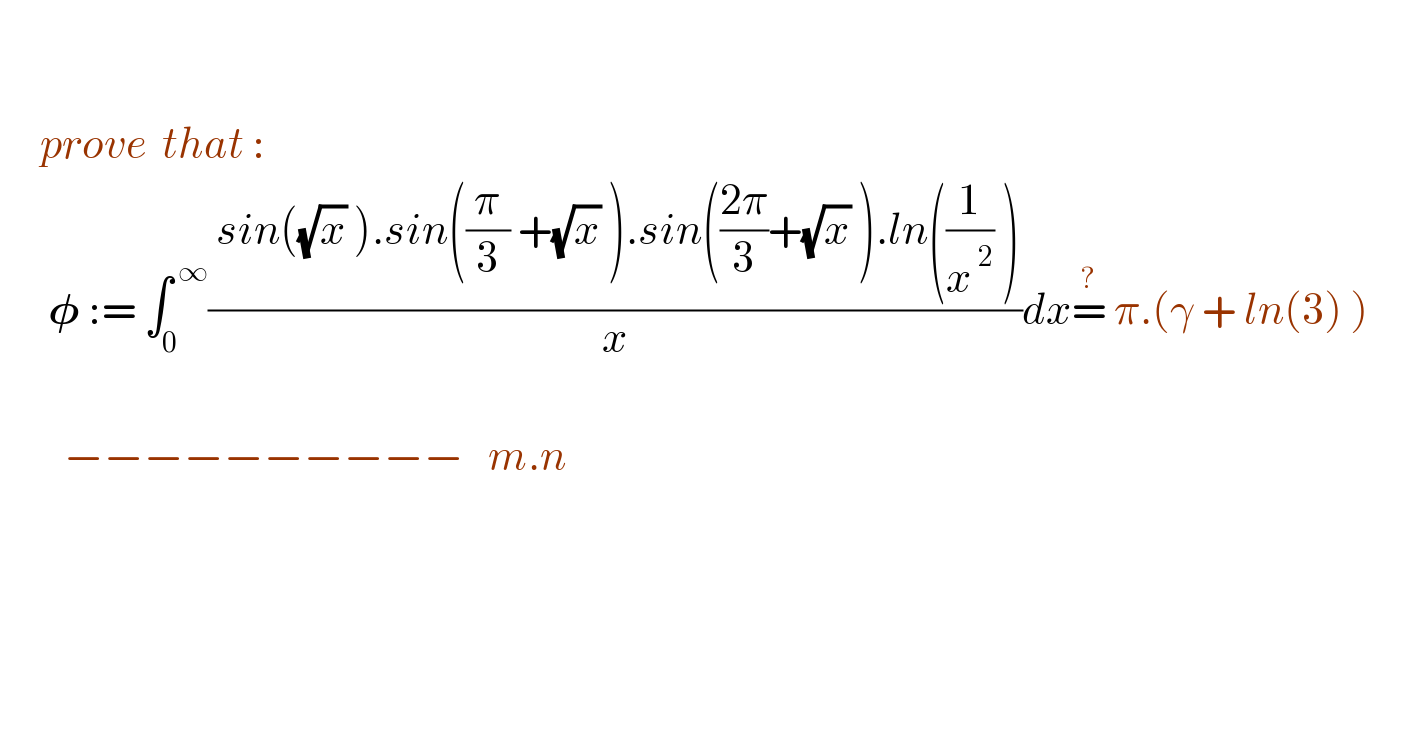
prove that : 𝛗 := ∫_0 ^( ∞) (( sin((√x) ).sin((π/3) +(√x) ).sin(((2π)/3)+(√x) ).ln((1/x^( 2) ) ))/x)dx=^? π.(γ + ln(3) ) −−−−−−−−−− m.n
$$ \\ $$$$\:\: \\ $$$$\:\:\:\:\:{prove}\:\:{that}\:: \\ $$$$\:\:\:\:\:\:\boldsymbol{\phi}\::=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:{sin}\left(\sqrt{{x}}\:\right).{sin}\left(\frac{\pi}{\mathrm{3}}\:+\sqrt{{x}}\:\right).{sin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}+\sqrt{{x}}\:\right).{ln}\left(\frac{\mathrm{1}}{{x}^{\:\mathrm{2}} }\:\right)}{{x}}{dx}\overset{?} {=}\:\pi.\left(\gamma\:+\:{ln}\left(\mathrm{3}\right)\:\right)\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:−−−−−−−−−−\:\:\:{m}.{n} \\ $$$$ \\ $$
Answered by mindispower last updated on 19/Nov/21
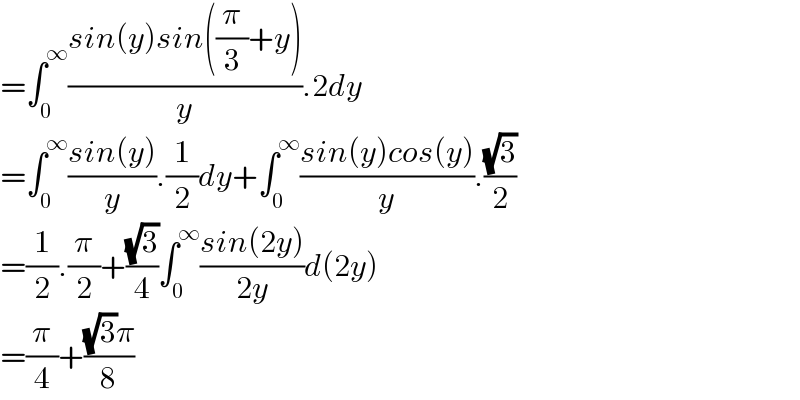
=∫_0 ^∞ ((sin(y)sin((π/3)+y))/y).2dy =∫_0 ^∞ ((sin(y))/y).(1/2)dy+∫_0 ^∞ ((sin(y)cos(y))/y).((√3)/2) =(1/2).(π/2)+((√3)/4)∫_0 ^∞ ((sin(2y))/(2y))d(2y) =(π/4)+(((√3)π)/8)
$$=\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({y}\right){sin}\left(\frac{\pi}{\mathrm{3}}+{y}\right)}{{y}}.\mathrm{2}{dy} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({y}\right)}{{y}}.\frac{\mathrm{1}}{\mathrm{2}}{dy}+\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({y}\right){cos}\left({y}\right)}{{y}}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\pi}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left(\mathrm{2}{y}\right)}{\mathrm{2}{y}}{d}\left(\mathrm{2}{y}\right) \\ $$$$=\frac{\pi}{\mathrm{4}}+\frac{\sqrt{\mathrm{3}}\pi}{\mathrm{8}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *