Question Number 173424 by mnjuly1970 last updated on 11/Jul/22
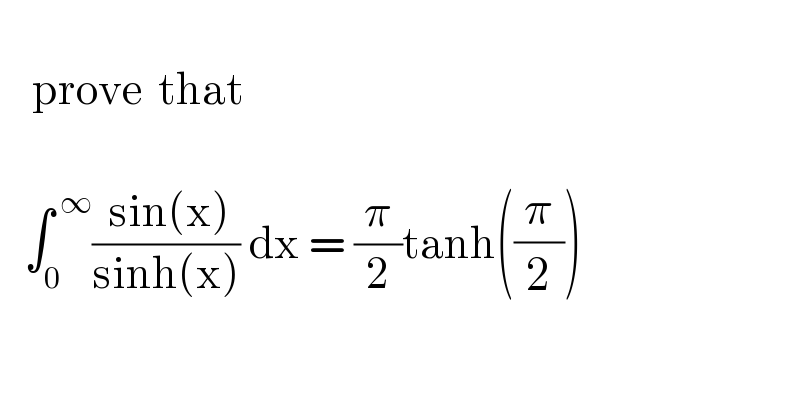
$$ \\ $$$$\:\:\:\:\mathrm{prove}\:\:\mathrm{that} \\ $$$$ \\ $$$$\:\:\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{sinh}\left(\mathrm{x}\right)}\:\mathrm{dx}\:=\:\frac{\pi}{\mathrm{2}}\mathrm{tanh}\left(\frac{\pi}{\mathrm{2}}\right) \\ $$$$ \\ $$
Answered by Mathspace last updated on 11/Jul/22
![Ψ=∫_0 ^∞ ((sinx)/(sh(x)))dx=2∫_0 ^∞ ((sinx)/(e^x −e^(−x) ))dx =2∫_0 ^∞ ((e^(−x) sinx)/(1−e^(−2x) ))dx =2∫_0 ^∞ e^(−x) sinxΣ_(n=0) ^∞ e^(−2nx) dx =2Σ_(n=0) ^∞ ∫_0 ^∞ e^(−(2n+1)x) sinx dx but ∫_0 ^∞ e^(−(2n+1)x) sinxdx =Im(∫_0 ^∞ e^(−(n+1)x+ix) dx) and ∫_0 ^∞ e^(−(n+1)+i)x) dx =(1/(−(n+1)+i))e^(−(n+1)+i)x) ]_0 ^∞ =(1/(n+1−i))=((n+1+i)/((n+1)^2 +1)) ⇒ Im(∫_0 ^∞ ....)=(1/((n+1)^2 +1)) ⇒ Ψ=2Σ_(n=0) ^∞ (1/((n+1)^2 +1)) =2Σ_(n=1) ^∞ (1/(n^2 +1)) Σ_(n=0) ^∞ (1/(n^2 +1))=Σ_(n=0) ^∞ (1/((n+i)(n−i))) =((Ψ(i)−Ψ(−i))/(2i)) after we use Ψ(z)−Ψ(1−z)=πcotan(πz) or we can developp cos(αx) at fourier serie to find the value...](https://www.tinkutara.com/question/Q173427.png)
$$\Psi=\int_{\mathrm{0}} ^{\infty} \:\frac{{sinx}}{{sh}\left({x}\right)}{dx}=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\frac{{sinx}}{{e}^{{x}} −{e}^{−{x}} }{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{x}} {sinx}}{\mathrm{1}−{e}^{−\mathrm{2}{x}} }{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} {sinx}\sum_{{n}=\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{nx}} {dx} \\ $$$$=\mathrm{2}\sum_{{n}=\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} {e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right){x}} {sinx}\:{dx} \\ $$$${but}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right){x}} {sinxdx} \\ $$$$={Im}\left(\int_{\mathrm{0}} ^{\infty} \:{e}^{−\left({n}+\mathrm{1}\right){x}+{ix}} {dx}\right) \\ $$$${and}\:\int_{\mathrm{0}} ^{\infty} {e}^{\left.−\left({n}+\mathrm{1}\right)+{i}\right){x}} {dx} \\ $$$$\left.=\frac{\mathrm{1}}{−\left({n}+\mathrm{1}\right)+{i}}{e}^{\left.−\left({n}+\mathrm{1}\right)+{i}\right){x}} \right]_{\mathrm{0}} ^{\infty} \\ $$$$=\frac{\mathrm{1}}{{n}+\mathrm{1}−{i}}=\frac{{n}+\mathrm{1}+{i}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}\:\Rightarrow \\ $$$${Im}\left(\int_{\mathrm{0}} ^{\infty} ….\right)=\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}\:\Rightarrow \\ $$$$\Psi=\mathrm{2}\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\mathrm{2}\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{1}}=\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left({n}+{i}\right)\left({n}−{i}\right)} \\ $$$$=\frac{\Psi\left({i}\right)−\Psi\left(−{i}\right)}{\mathrm{2}{i}}\:{after}\:{we}\:{use} \\ $$$$\Psi\left({z}\right)−\Psi\left(\mathrm{1}−{z}\right)=\pi{cotan}\left(\pi{z}\right) \\ $$$${or}\:{we}\:{can}\:{developp}\:{cos}\left(\alpha{x}\right) \\ $$$${at}\:{fourier}\:{serie}\:{to}\:{find}\:{the}\:{value}… \\ $$
Commented by mnjuly1970 last updated on 11/Jul/22

$$\mathrm{grateful}\:\mathrm{sir}\: \\ $$
Commented by Tawa11 last updated on 13/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
