Question Number 25183 by ajfour last updated on 06/Dec/17
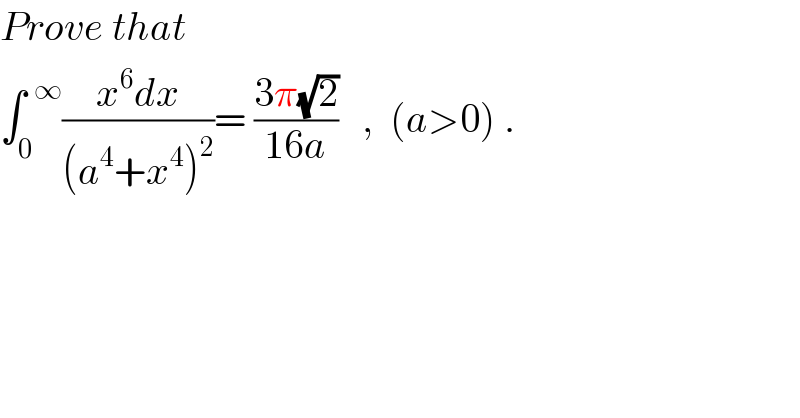
$${Prove}\:{that} \\ $$$$\int_{\mathrm{0}} ^{\:\:\infty} \frac{{x}^{\mathrm{6}} {dx}}{\left({a}^{\mathrm{4}} +{x}^{\mathrm{4}} \right)^{\mathrm{2}} }=\:\frac{\mathrm{3}\pi\sqrt{\mathrm{2}}}{\mathrm{16}{a}}\:\:\:,\:\:\left({a}>\mathrm{0}\right)\:. \\ $$
Commented by prakash jain last updated on 05/Dec/17
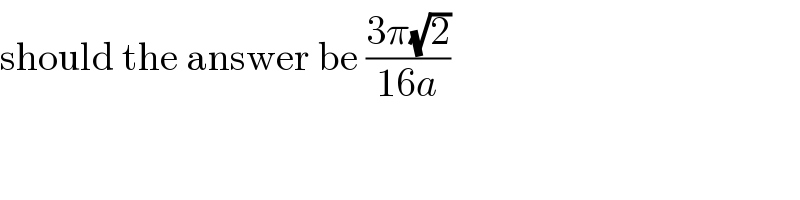
$$\mathrm{should}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{be}\:\frac{\mathrm{3}\pi\sqrt{\mathrm{2}}}{\mathrm{16}{a}} \\ $$
