Menu Close

prove-that-0-x-sinh-x-3-dx-2-16-12-2-written-and-prepared-by-m-n-

Tinku Tara 0 Comments
Pin




Question Number 174696 by mnjuly1970 last updated on 08/Aug/22
prove that : 𝛀 = ∫_0 ^( ∞) ( (( x)/( sinh (x))) )^( 3) dx =(𝛑^( 2) /(16)) (12βˆ’ 𝛑^( 2) ) written and prepared by : m.n
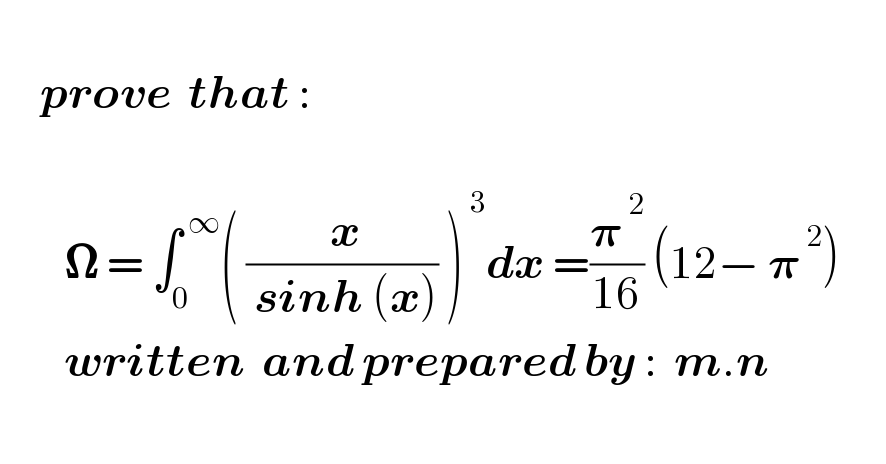
$$ \\ $$$$\:\:\:\:\:\boldsymbol{{prove}}\:\:\boldsymbol{{that}}\:: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\boldsymbol{\Omega}\:=\:\int_{\mathrm{0}} ^{\:\infty} \left(\:\frac{\:\boldsymbol{{x}}}{\:\boldsymbol{{sinh}}\:\left(\boldsymbol{{x}}\right)}\:\right)^{\:\mathrm{3}} \boldsymbol{{dx}}\:=\frac{\boldsymbol{\pi}^{\:\mathrm{2}} }{\mathrm{16}}\:\left(\mathrm{12}βˆ’\:\boldsymbol{\pi}^{\:\mathrm{2}} \right)\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\boldsymbol{{written}}\:\:\boldsymbol{{and}}\:\boldsymbol{{prepared}}\:\boldsymbol{{by}}\::\:\:\boldsymbol{{m}}.\boldsymbol{{n}}\:\:\:\:\:\:\:\: \\ $$$$ \\ $$
Answered by aleks041103 last updated on 08/Aug/22
(1/((1βˆ’x)^3 ))=(1/2) (d^2 /dx^2 )((1/(1βˆ’x)))=(1/2) (d^2 /dx^2 )(Ξ£_(i=0) ^∞ x^i )= =(1/2)(Ξ£_(i=2) ^∞ ((i!)/((iβˆ’2)!))x^(iβˆ’2) ) (1/(sinh^3 x))=(((2e^(βˆ’x) )/(1βˆ’e^(βˆ’2x) )))^3 =8e^(βˆ’3x) ((1/(1βˆ’r)))^3 = =4e^(βˆ’3x) Ξ£_(i=0) ^∞ (((i+2)!)/(i!))r^i = =4e^(βˆ’3x) Ξ£_(i=0) ^∞ (((i+2)!)/(i!))e^(βˆ’2ix) =4Ξ£_(i=0) ^∞ (((i+2)!)/(i!))e^(βˆ’(2i+3)x) ∫_0 ^∞ ((x^3 dx)/(sinh^3 x))=4Ξ£_(i=0) ^∞ (((i+2)!)/(i!))∫_0 ^∞ x^3 e^(βˆ’(2i+3)x) dx ∫_0 ^∞ x^3 e^(βˆ’(2i+3)x) dx=(1/((2i+3)^4 ))∫_0 ^∞ z^3 e^(βˆ’z) dz=(6/((2i+3)^4 )) β‡’Ans.=24Ξ£_(i=0) ^∞ (((i+1)(i+2))/((2i+3)^4 ))= =24Ξ£_(i=1) ^∞ ((i(i+1))/((2i+1)^4 )) ((i(i+1))/((2i+1)^4 ))=((i^2 +i)/((2i+1)^4 ))=((i^2 +2.(1/2).i+((1/2))^2 βˆ’((1/2))^2 )/((2i+1)^4 ))= =(((i+(1/2))^2 βˆ’(1/4))/((2i+1)^4 ))=(1/4) (((2i+1)^2 )/((2i+1)^4 ))βˆ’(1/4) (1/((2i+1)^4 ))= =(1/4)((1/((2i+1)^2 ))βˆ’(1/((2i+1)^4 ))) β‡’Ans.=6[Ξ£_(i=1) ^∞ (1/((2i+1)^2 ))βˆ’Ξ£_(i=1) ^∞ (1/((2i+1)^4 ))] Ξ£_(i=1) ^∞ (1/((2i+1)^n ))=Ξ£_(i=1) ^∞ ((1/((2i+1)^n ))+(1/((2i)^n )))βˆ’Ξ£_(i=1) ^∞ (1/((2i)^n ))= =Ξ£_(i=2) ^∞ (1/((i)^n ))βˆ’2^(βˆ’n) Ξ£_(i=1) ^∞ (1/i^n )= =Ξ£_(i=1) ^∞ (1/i^n )βˆ’1βˆ’2^(βˆ’n) Ξ£_(i=1) ^∞ (1/i^n )= =(1βˆ’2^(βˆ’n) )ΞΆ(n)βˆ’1 β‡’Ans.=6((1βˆ’2^(βˆ’2) )ΞΆ(2)βˆ’(1βˆ’2^(βˆ’4) )ΞΆ(4))= =6((3/4) (Ο€^2 /6)βˆ’((15)/(16)) (Ο€^4 /(90)))= =(3/4)Ο€^2 βˆ’(1/(16))Ο€^4 = =(Ο€^2 /(16))(12βˆ’Ο€^2 )
$$\frac{\mathrm{1}}{\left(\mathrm{1}βˆ’{x}\right)^{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{2}}\:\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }\left(\frac{\mathrm{1}}{\mathrm{1}βˆ’{x}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\:\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }\left(\underset{{i}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{i}} \right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\underset{{i}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{{i}!}{\left({i}βˆ’\mathrm{2}\right)!}{x}^{{i}βˆ’\mathrm{2}} \right) \\ $$$$\frac{\mathrm{1}}{{sinh}^{\mathrm{3}} {x}}=\left(\frac{\mathrm{2}{e}^{βˆ’{x}} }{\mathrm{1}βˆ’{e}^{βˆ’\mathrm{2}{x}} }\right)^{\mathrm{3}} =\mathrm{8}{e}^{βˆ’\mathrm{3}{x}} \left(\frac{\mathrm{1}}{\mathrm{1}βˆ’{r}}\right)^{\mathrm{3}} = \\ $$$$=\mathrm{4}{e}^{βˆ’\mathrm{3}{x}} \underset{{i}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left({i}+\mathrm{2}\right)!}{{i}!}{r}^{{i}} = \\ $$$$=\mathrm{4}{e}^{βˆ’\mathrm{3}{x}} \underset{{i}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left({i}+\mathrm{2}\right)!}{{i}!}{e}^{βˆ’\mathrm{2}{ix}} =\mathrm{4}\underset{{i}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left({i}+\mathrm{2}\right)!}{{i}!}{e}^{βˆ’\left(\mathrm{2}{i}+\mathrm{3}\right){x}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{3}} {dx}}{{sinh}^{\mathrm{3}} {x}}=\mathrm{4}\underset{{i}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left({i}+\mathrm{2}\right)!}{{i}!}\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{3}} {e}^{βˆ’\left(\mathrm{2}{i}+\mathrm{3}\right){x}} {dx} \\ $$$$\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{3}} {e}^{βˆ’\left(\mathrm{2}{i}+\mathrm{3}\right){x}} {dx}=\frac{\mathrm{1}}{\left(\mathrm{2}{i}+\mathrm{3}\right)^{\mathrm{4}} }\int_{\mathrm{0}} ^{\infty} {z}^{\mathrm{3}} {e}^{βˆ’{z}} {dz}=\frac{\mathrm{6}}{\left(\mathrm{2}{i}+\mathrm{3}\right)^{\mathrm{4}} } \\ $$$$\Rightarrow{Ans}.=\mathrm{24}\underset{{i}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left({i}+\mathrm{1}\right)\left({i}+\mathrm{2}\right)}{\left(\mathrm{2}{i}+\mathrm{3}\right)^{\mathrm{4}} }= \\ $$$$=\mathrm{24}\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{i}\left({i}+\mathrm{1}\right)}{\left(\mathrm{2}{i}+\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$\frac{{i}\left({i}+\mathrm{1}\right)}{\left(\mathrm{2}{i}+\mathrm{1}\right)^{\mathrm{4}} }=\frac{{i}^{\mathrm{2}} +{i}}{\left(\mathrm{2}{i}+\mathrm{1}\right)^{\mathrm{4}} }=\frac{{i}^{\mathrm{2}} +\mathrm{2}.\frac{\mathrm{1}}{\mathrm{2}}.{i}+\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} βˆ’\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }{\left(\mathrm{2}{i}+\mathrm{1}\right)^{\mathrm{4}} }= \\ $$$$=\frac{\left({i}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} βˆ’\frac{\mathrm{1}}{\mathrm{4}}}{\left(\mathrm{2}{i}+\mathrm{1}\right)^{\mathrm{4}} }=\frac{\mathrm{1}}{\mathrm{4}}\:\frac{\left(\mathrm{2}{i}+\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{2}{i}+\mathrm{1}\right)^{\mathrm{4}} }βˆ’\frac{\mathrm{1}}{\mathrm{4}}\:\frac{\mathrm{1}}{\left(\mathrm{2}{i}+\mathrm{1}\right)^{\mathrm{4}} }= \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{\left(\mathrm{2}{i}+\mathrm{1}\right)^{\mathrm{2}} }βˆ’\frac{\mathrm{1}}{\left(\mathrm{2}{i}+\mathrm{1}\right)^{\mathrm{4}} }\right) \\ $$$$\Rightarrow{Ans}.=\mathrm{6}\left[\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{i}+\mathrm{1}\right)^{\mathrm{2}} }βˆ’\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{i}+\mathrm{1}\right)^{\mathrm{4}} }\right] \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{i}+\mathrm{1}\right)^{{n}} }=\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\left(\mathrm{2}{i}+\mathrm{1}\right)^{{n}} }+\frac{\mathrm{1}}{\left(\mathrm{2}{i}\right)^{{n}} }\right)βˆ’\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{i}\right)^{{n}} }= \\ $$$$=\underset{{i}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({i}\right)^{{n}} }βˆ’\mathrm{2}^{βˆ’{n}} \underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{i}^{{n}} }= \\ $$$$=\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{i}^{{n}} }βˆ’\mathrm{1}βˆ’\mathrm{2}^{βˆ’{n}} \underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{i}^{{n}} }= \\ $$$$=\left(\mathrm{1}βˆ’\mathrm{2}^{βˆ’{n}} \right)\zeta\left({n}\right)βˆ’\mathrm{1} \\ $$$$\Rightarrow{Ans}.=\mathrm{6}\left(\left(\mathrm{1}βˆ’\mathrm{2}^{βˆ’\mathrm{2}} \right)\zeta\left(\mathrm{2}\right)βˆ’\left(\mathrm{1}βˆ’\mathrm{2}^{βˆ’\mathrm{4}} \right)\zeta\left(\mathrm{4}\right)\right)= \\ $$$$=\mathrm{6}\left(\frac{\mathrm{3}}{\mathrm{4}}\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}βˆ’\frac{\mathrm{15}}{\mathrm{16}}\:\frac{\pi^{\mathrm{4}} }{\mathrm{90}}\right)= \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}\pi^{\mathrm{2}} βˆ’\frac{\mathrm{1}}{\mathrm{16}}\pi^{\mathrm{4}} = \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{16}}\left(\mathrm{12}βˆ’\pi^{\mathrm{2}} \right) \\ $$
Commented by aleks041103 last updated on 08/Aug/22
I did it finally... 🀣🀣
$${I}\:{did}\:{it}\:{finally}… \\ $$🀣🀣
Commented by mnjuly1970 last updated on 09/Aug/22
thanks alot sir aleks...i appreciate
$${thanks}\:{alot} \\ $$$${sir}\:{aleks}…{i}\:{appreciate} \\ $$
Commented by Tawa11 last updated on 09/Aug/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by princeDera last updated on 09/Aug/22
Ξ© ∫_0 ^∞ ((x/(sinh (x))))^3 = 8∫_0 ^∞ (((xe^(βˆ’x) )/(1βˆ’e^(βˆ’2x) )))^3 Ξ© = 8∫_0 ^∞ ((x^3 e^(βˆ’3x) )/((1βˆ’e^(βˆ’2x) )^3 )) = 4∫_0 ^∞ x^3 e^(βˆ’3x) Ξ£_(kβ‰₯0) (2+k)(1+k)e^(βˆ’2kx) dx Ξ© =4Ξ£_(kβ‰₯0) (2+3k+k^2 )∫_0 ^∞ x^3 e^(βˆ’(3+2k)x) dx Ξ© = 8Ξ£_(kβ‰₯0) (6/((3+2k)^4 )) + 24Ξ£_(kβ‰₯0) (((k + (3/2))^2 βˆ’ (9/4))/((2k+3)^4 )) Ξ© = 48Ξ£_(kβ‰₯1) (1/((2k+1)^4 )) + 6Ξ£_(kβ‰₯0) (((2k+3)^2 )/((2k+3)^4 )) βˆ’ 54Ξ£_(kβ‰₯0) (1/((2k+3)^4 )) Ξ© = 48(Ξ»(4)βˆ’1) + 6Ξ»(2)βˆ’6 βˆ’ 54Ξ»(4) + 54 Ξ© = 48{(Ο€^4 /(96))βˆ’1} + ((6Ο€^2 )/8) βˆ’ 6 βˆ’ 54.(Ο€^4 /(96)) +54 Ξ© = (Ο€^4 /(96))(48βˆ’54) + ((3Ο€^2 )/4) = ((3Ο€^2 )/(4 )) βˆ’ (Ο€^4 /(16)) Ξ© = (Ο€^2 /(16))(12βˆ’Ο€^2 ) Ξ»(x) is dirichlet lambda function
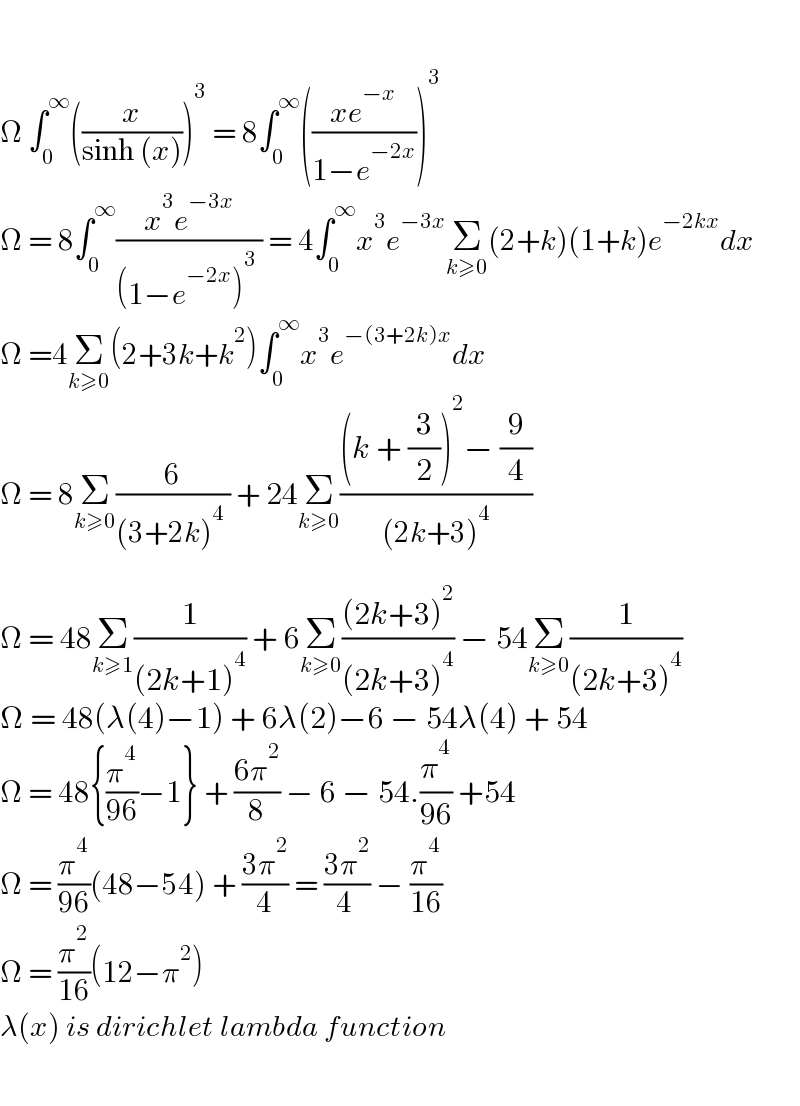
$$ \\ $$$$ \\ $$$$\Omega\:\int_{\mathrm{0}} ^{\infty} \left(\frac{{x}}{\mathrm{sinh}\:\left({x}\right)}\right)^{\mathrm{3}} \:=\:\mathrm{8}\int_{\mathrm{0}} ^{\infty} \left(\frac{{xe}^{βˆ’{x}} }{\mathrm{1}βˆ’{e}^{βˆ’\mathrm{2}{x}} }\right)^{\mathrm{3}} \\ $$$$\Omega\:=\:\mathrm{8}\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{3}} {e}^{βˆ’\mathrm{3}{x}} }{\left(\mathrm{1}βˆ’{e}^{βˆ’\mathrm{2}{x}} \right)^{\mathrm{3}} \:}\:=\:\mathrm{4}\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{3}} {e}^{βˆ’\mathrm{3}{x}} \underset{{k}\geqslant\mathrm{0}} {\sum}\left(\mathrm{2}+{k}\right)\left(\mathrm{1}+{k}\right){e}^{βˆ’\mathrm{2}{kx}} {dx} \\ $$$$\Omega\:=\mathrm{4}\underset{{k}\geqslant\mathrm{0}} {\sum}\left(\mathrm{2}+\mathrm{3}{k}+{k}^{\mathrm{2}} \right)\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{3}} {e}^{βˆ’\left(\mathrm{3}+\mathrm{2}{k}\right){x}} {dx} \\ $$$$\Omega\:=\:\mathrm{8}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{6}}{\left(\mathrm{3}+\mathrm{2}{k}\right)^{\mathrm{4}} \:}\:+\:\mathrm{24}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left({k}\:+\:\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} βˆ’\:\frac{\mathrm{9}}{\mathrm{4}}}{\left(\mathrm{2}{k}+\mathrm{3}\right)^{\mathrm{4}} } \\ $$$$ \\ $$$$\Omega\:=\:\mathrm{48}\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{4}} }\:+\:\mathrm{6}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(\mathrm{2}{k}+\mathrm{3}\right)^{\mathrm{2}} }{\left(\mathrm{2}{k}+\mathrm{3}\right)^{\mathrm{4}} }\:βˆ’\:\mathrm{54}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{3}\right)^{\mathrm{4}} } \\ $$$$\Omega\:=\:\mathrm{48}\left(\lambda\left(\mathrm{4}\right)βˆ’\mathrm{1}\right)\:+\:\mathrm{6}\lambda\left(\mathrm{2}\right)βˆ’\mathrm{6}\:βˆ’\:\mathrm{54}\lambda\left(\mathrm{4}\right)\:+\:\mathrm{54} \\ $$$$\Omega\:=\:\mathrm{48}\left\{\frac{\pi^{\mathrm{4}} }{\mathrm{96}}βˆ’\mathrm{1}\right\}\:+\:\frac{\mathrm{6}\pi^{\mathrm{2}} }{\mathrm{8}}\:βˆ’\:\mathrm{6}\:βˆ’\:\mathrm{54}.\frac{\pi^{\mathrm{4}} }{\mathrm{96}}\:+\mathrm{54}\: \\ $$$$\Omega\:=\:\frac{\pi^{\mathrm{4}} }{\mathrm{96}}\left(\mathrm{48}βˆ’\mathrm{54}\right)\:+\:\frac{\mathrm{3}\pi^{\mathrm{2}} }{\mathrm{4}}\:=\:\frac{\mathrm{3}\pi^{\mathrm{2}} }{\mathrm{4}\:}\:βˆ’\:\frac{\pi^{\mathrm{4}} }{\mathrm{16}}\: \\ $$$$\Omega\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{16}}\left(\mathrm{12}βˆ’\pi^{\mathrm{2}} \right) \\ $$$$\lambda\left({x}\right)\:{is}\:{dirichlet}\:{lambda}\:{function} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 09/Aug/22
grateful sir
$${grateful}\:{sir} \\ $$$$ \\ $$
Commented by Tawa11 last updated on 09/Aug/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by Ar Brandon last updated on 09/Aug/22
Ξ©=∫_0 ^∞ ((x/(sinhx)))^3 dx=∫_0 ^∞ (x^3 /(sinh^3 x))dx=8∫_0 ^∞ (x^3 /((e^x βˆ’e^(βˆ’x) )^3 ))dx =8∫_0 ^∞ ((x^3 e^(βˆ’3x) )/((1βˆ’e^(βˆ’2x) )^3 ))dx=4∫_0 ^∞ x^3 e^(βˆ’3x) Ξ£_(n=0) ^∞ (n+1)(n+2)e^(βˆ’2nx) dx ======================================= (1/(1βˆ’t))=Ξ£_(n=0) ^∞ t^n β‡’(1/((1βˆ’t)^2 ))=Ξ£_(n=0) ^∞ nt^(nβˆ’1) =Ξ£_(n=0) ^∞ (n+1)t^n β‡’(2/((1βˆ’t)^3 ))=Ξ£_(n=0) ^∞ n(n+1)t^(nβˆ’1) =Ξ£_(n=0) ^∞ (n+1)(n+2)t^n ======================================= =4Ξ£_(n=0) ^∞ (n+1)(n+2)∫_0 ^∞ x^3 e^(βˆ’(2n+3)x) dx=4Ξ£_(n=0) ^∞ (((n+1)(n+2))/((2n+3)^4 ))∫_0 ^∞ x^3 e^(βˆ’x) dx =Ξ£_(n=0) ^∞ (((2n+3βˆ’1)(2n+3+1))/((2n+3)^4 ))∫_0 ^∞ x^3 e^(βˆ’x) dx=Ξ£_(n=0) ^∞ (((2n+3)^2 βˆ’1)/((2n+3)^4 ))Ξ“(4) =6Ξ£_(n=0) ^∞ ((1/((2n+3)^2 ))βˆ’(1/((2n+3)^4 )))=6(Ξ£_(n=0) ^∞ (1/((2n+1)^2 ))βˆ’1βˆ’(Ξ£_(n=0) ^∞ (1/((2n+1)^4 ))βˆ’1)) =6((3/4)Γ—ΞΆ(2)βˆ’((15)/(16))Γ—ΞΆ(4))=6((3/4)Γ—(Ο€^2 /6)βˆ’((15)/(16))Γ—(Ο€^4 /(90)))=((3Ο€^2 )/4)βˆ’(Ο€^4 /(16))=(Ο€^2 /(16))(12βˆ’Ο€^2 )β˜…
$$\Omega=\int_{\mathrm{0}} ^{\infty} \left(\frac{{x}}{\mathrm{sinh}{x}}\right)^{\mathrm{3}} {dx}=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{3}} }{\mathrm{sinh}^{\mathrm{3}} {x}}{dx}=\mathrm{8}\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{3}} }{\left({e}^{{x}} βˆ’{e}^{βˆ’{x}} \right)^{\mathrm{3}} }{dx} \\ $$$$\:\:\:\:=\mathrm{8}\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{3}} {e}^{βˆ’\mathrm{3}{x}} }{\left(\mathrm{1}βˆ’{e}^{βˆ’\mathrm{2}{x}} \right)^{\mathrm{3}} }{dx}=\mathrm{4}\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{3}} {e}^{βˆ’\mathrm{3}{x}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right){e}^{βˆ’\mathrm{2}{nx}} {dx} \\ $$$$======================================= \\ $$$$\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}βˆ’{t}}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{t}^{{n}} \:\Rightarrow\frac{\mathrm{1}}{\left(\mathrm{1}βˆ’{t}\right)^{\mathrm{2}} }=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{nt}^{{n}βˆ’\mathrm{1}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left({n}+\mathrm{1}\right){t}^{{n}} \\ $$$$\:\:\:\:\:\Rightarrow\frac{\mathrm{2}}{\left(\mathrm{1}βˆ’{t}\right)^{\mathrm{3}} }=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{n}\left({n}+\mathrm{1}\right){t}^{{n}βˆ’\mathrm{1}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right){t}^{{n}} \\ $$$$======================================= \\ $$$$\:\:\:\:=\mathrm{4}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{3}} {e}^{βˆ’\left(\mathrm{2}{n}+\mathrm{3}\right){x}} {dx}=\mathrm{4}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{\left(\mathrm{2}{n}+\mathrm{3}\right)^{\mathrm{4}} }\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{3}} {e}^{βˆ’{x}} {dx} \\ $$$$\:\:\:\:=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{2}{n}+\mathrm{3}βˆ’\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{3}+\mathrm{1}\right)}{\left(\mathrm{2}{n}+\mathrm{3}\right)^{\mathrm{4}} }\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{3}} {e}^{βˆ’{x}} {dx}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{2}{n}+\mathrm{3}\right)^{\mathrm{2}} βˆ’\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{3}\right)^{\mathrm{4}} }\Gamma\left(\mathrm{4}\right) \\ $$$$\:\:\:\:=\mathrm{6}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{3}\right)^{\mathrm{2}} }βˆ’\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{3}\right)^{\mathrm{4}} }\right)=\mathrm{6}\left(\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }βˆ’\mathrm{1}βˆ’\left(\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{4}} }βˆ’\mathrm{1}\right)\right) \\ $$$$\:\:\:\:=\mathrm{6}\left(\frac{\mathrm{3}}{\mathrm{4}}Γ—\zeta\left(\mathrm{2}\right)βˆ’\frac{\mathrm{15}}{\mathrm{16}}Γ—\zeta\left(\mathrm{4}\right)\right)=\mathrm{6}\left(\frac{\mathrm{3}}{\mathrm{4}}Γ—\frac{\pi^{\mathrm{2}} }{\mathrm{6}}βˆ’\frac{\mathrm{15}}{\mathrm{16}}Γ—\frac{\pi^{\mathrm{4}} }{\mathrm{90}}\right)=\frac{\mathrm{3}\pi^{\mathrm{2}} }{\mathrm{4}}βˆ’\frac{\pi^{\mathrm{4}} }{\mathrm{16}}=\frac{\pi^{\mathrm{2}} }{\mathrm{16}}\left(\mathrm{12}βˆ’\pi^{\mathrm{2}} \right)\bigstar \\ $$
Commented by mnjuly1970 last updated on 09/Aug/22
thank you sir
$${thank}\:{you}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *