Question Number 33349 by caravan msup abdo. last updated on 14/Apr/18
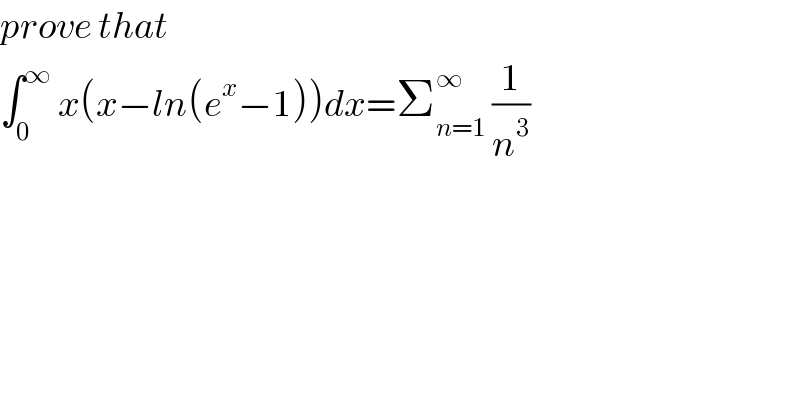
$${prove}\:{that}\: \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{x}\left({x}−{ln}\left({e}^{{x}} −\mathrm{1}\right)\right){dx}=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{3}} } \\ $$
Commented by math khazana by abdo last updated on 18/Apr/18
![let put I = ∫_0 ^∞ x(x −ln(e^x −1))dx I = ∫_0 ^∞ x( x −ln(e^x (1−e^(−x) ))dx = −∫_0 ^∞ x ln(1−e^(−x) )dx but we have (1/(1−u))= Σ_(n=0) ^∞ u^n ⇒ −ln(1−u) =Σ_(n=0) ^∞ (u^(n+1) /(n+1)) = Σ_(n=1) ^∞ (u^n /n) ⇒ −ln(1−e^(−x) ) = Σ_(n=1) ^∞ (e^(−nx) /n) I = ∫_0 ^∞ (Σ_(n=1) ^∞ (e^(−nx) /n))x dx = Σ_(n=1) ^∞ (1/n)∫_0 ^∞ x e^(−nx) dx ∫_0 ^∞ x e^(−nx) dx =_(nx =t) ∫_0 ^∞ (t/n) e^(−t) (dt/n) =(1/n^2 ) ∫_0 ^∞ t e^(−t) dt and by parts ∫_0 ^∞ t e^(−t) dt = [−t e^(−t) ]_0 ^(+∞) +∫_0 ^∞ e^(−t) dt =[ −e^(−t) ]_0 ^(+∞) =1 ⇒ I = Σ_(n=1) ^∞ (1/n^3 ) .](https://www.tinkutara.com/question/Q33525.png)
$${let}\:{put}\:{I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:{x}\left({x}\:−{ln}\left({e}^{{x}} \:−\mathrm{1}\right)\right){dx} \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:{x}\left(\:{x}\:−{ln}\left({e}^{{x}} \left(\mathrm{1}−{e}^{−{x}} \right)\right){dx}\right. \\ $$$$=\:−\int_{\mathrm{0}} ^{\infty} \:\:{x}\:\:{ln}\left(\mathrm{1}−{e}^{−{x}} \right){dx}\:\:{but}\:{we}\:{have} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−{u}}=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:{u}^{{n}} \:\:\Rightarrow\:−{ln}\left(\mathrm{1}−{u}\right)\:\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{u}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}} \\ $$$$=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{u}^{{n}} }{{n}}\:\Rightarrow\:−{ln}\left(\mathrm{1}−{e}^{−{x}} \right)\:=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{e}^{−{nx}} }{{n}} \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{\infty} \left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{e}^{−{nx}} }{{n}}\right){x}\:{dx} \\ $$$$=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\infty} \:\:{x}\:{e}^{−{nx}} \:{dx}\:\:\:\: \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{x}\:{e}^{−{nx}} \:{dx}\:=_{{nx}\:={t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{{t}}{{n}}\:{e}^{−{t}} \:\:\frac{{dt}}{{n}} \\ $$$$=\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\infty} \:{t}\:{e}^{−{t}} {dt}\:\:\:{and}\:{by}\:{parts} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:{t}\:{e}^{−{t}} {dt}\:=\:\left[−{t}\:{e}^{−{t}} \right]_{\mathrm{0}} ^{+\infty} \:+\int_{\mathrm{0}} ^{\infty} \:{e}^{−{t}} {dt} \\ $$$$=\left[\:−{e}^{−{t}} \right]_{\mathrm{0}} ^{+\infty} \:=\mathrm{1}\:\:\Rightarrow\:\:{I}\:\:=\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:\:. \\ $$
