Question Number 144199 by qaz last updated on 23/Jun/21
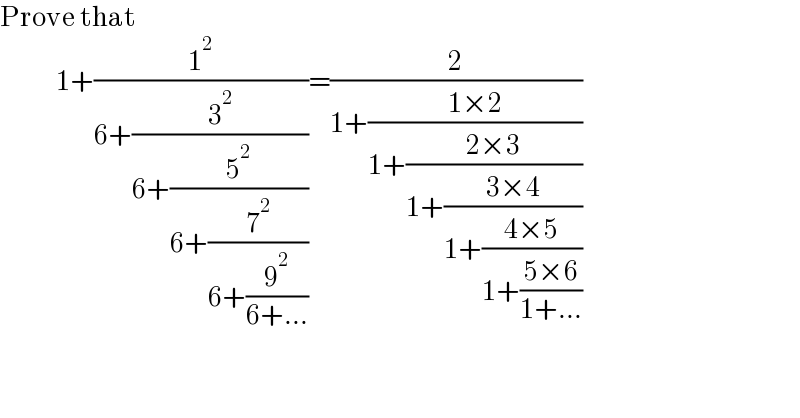
$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}+\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{6}+\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{6}+\frac{\mathrm{5}^{\mathrm{2}} }{\mathrm{6}+\frac{\mathrm{7}^{\mathrm{2}} }{\mathrm{6}+\frac{\mathrm{9}^{\mathrm{2}} }{\mathrm{6}+…}}}}}=\frac{\mathrm{2}}{\mathrm{1}+\frac{\mathrm{1}×\mathrm{2}}{\mathrm{1}+\frac{\mathrm{2}×\mathrm{3}}{\mathrm{1}+\frac{\mathrm{3}×\mathrm{4}}{\mathrm{1}+\frac{\mathrm{4}×\mathrm{5}}{\mathrm{1}+\frac{\mathrm{5}×\mathrm{6}}{\mathrm{1}+…}}}}}} \\ $$
Answered by Dwaipayan Shikari last updated on 23/Jun/21
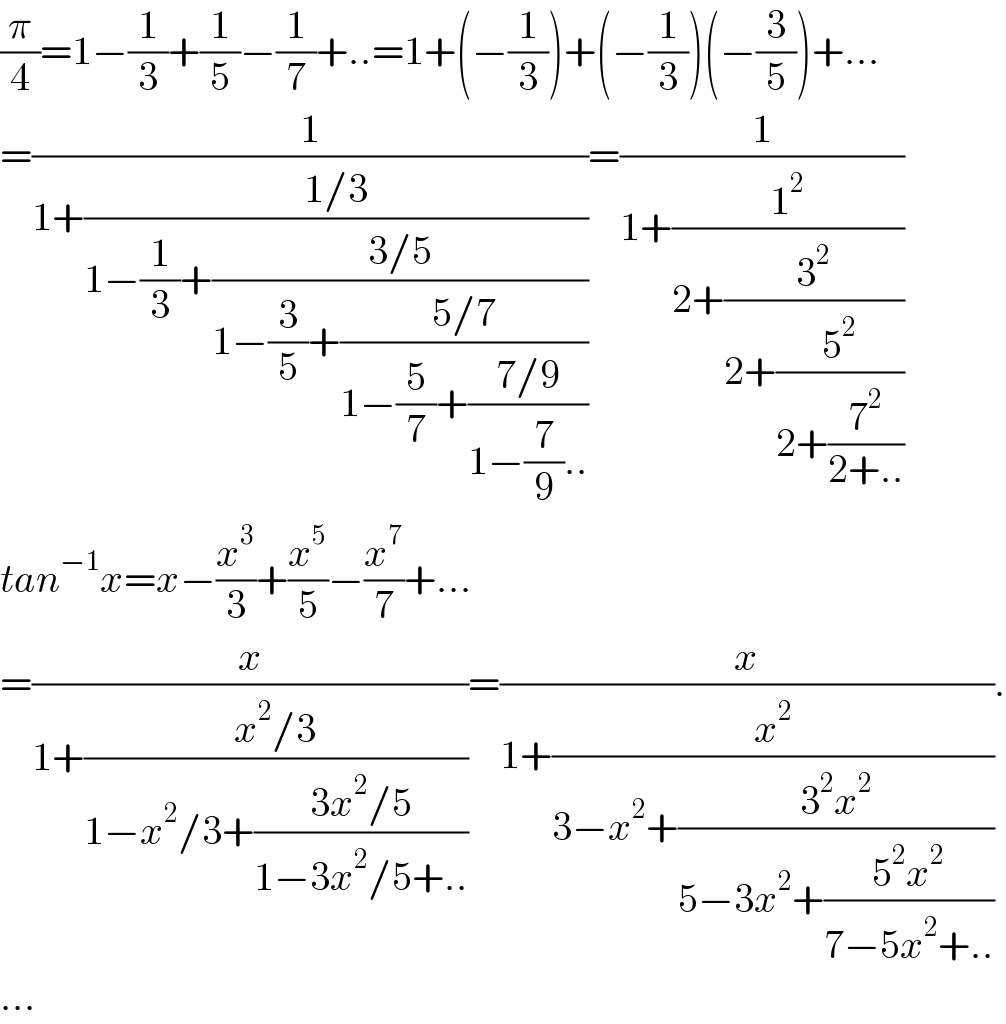
$$\frac{\pi}{\mathrm{4}}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{7}}+..=\mathrm{1}+\left(−\frac{\mathrm{1}}{\mathrm{3}}\right)+\left(−\frac{\mathrm{1}}{\mathrm{3}}\right)\left(−\frac{\mathrm{3}}{\mathrm{5}}\right)+… \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}/\mathrm{3}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{3}/\mathrm{5}}{\mathrm{1}−\frac{\mathrm{3}}{\mathrm{5}}+\frac{\mathrm{5}/\mathrm{7}}{\mathrm{1}−\frac{\mathrm{5}}{\mathrm{7}}+\frac{\mathrm{7}/\mathrm{9}}{\mathrm{1}−\frac{\mathrm{7}}{\mathrm{9}}..}}}}}=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{2}+\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{2}+\frac{\mathrm{5}^{\mathrm{2}} }{\mathrm{2}+\frac{\mathrm{7}^{\mathrm{2}} }{\mathrm{2}+..}}}}} \\ $$$${tan}^{−\mathrm{1}} {x}={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}}−\frac{{x}^{\mathrm{7}} }{\mathrm{7}}+… \\ $$$$=\frac{{x}}{\mathrm{1}+\frac{{x}^{\mathrm{2}} /\mathrm{3}}{\mathrm{1}−{x}^{\mathrm{2}} /\mathrm{3}+\frac{\mathrm{3}{x}^{\mathrm{2}} /\mathrm{5}}{\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} /\mathrm{5}+..}}}=\frac{{x}}{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}−{x}^{\mathrm{2}} +\frac{\mathrm{3}^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{5}−\mathrm{3}{x}^{\mathrm{2}} +\frac{\mathrm{5}^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{7}−\mathrm{5}{x}^{\mathrm{2}} +..}}}}. \\ $$$$… \\ $$
