Question Number 185973 by normans last updated on 30/Jan/23
![[prove that;] 1 + 2 = 3](https://www.tinkutara.com/question/Q185973.png)
Commented by MJS_new last updated on 30/Jan/23
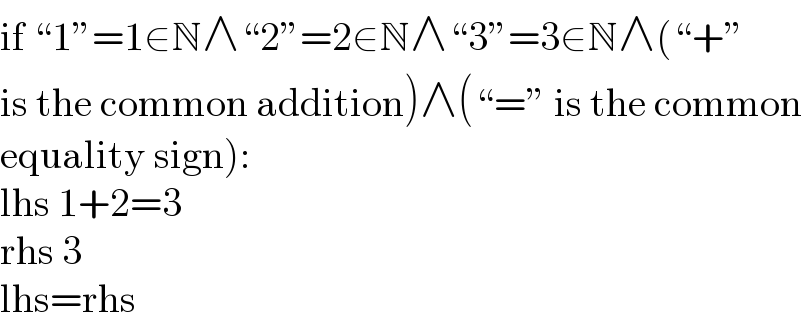
Commented by MJS_new last updated on 30/Jan/23
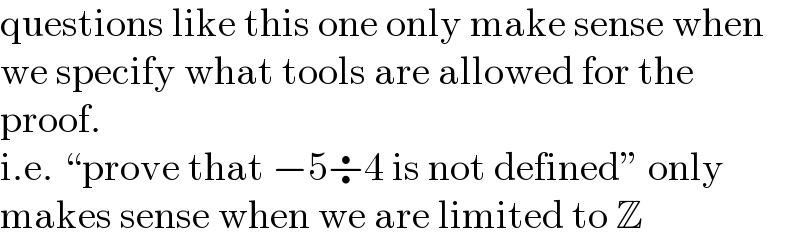
Answered by Mathspace last updated on 30/Jan/23
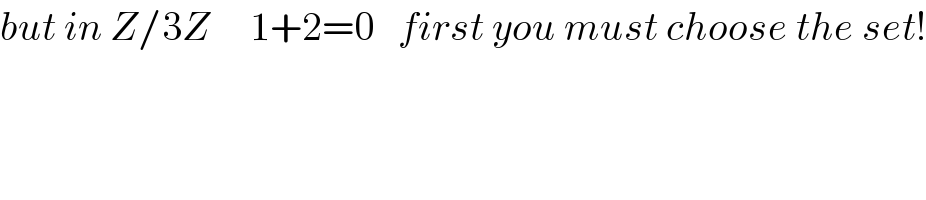
Commented by MJS_new last updated on 30/Jan/23

