Question Number 104092 by naka3546 last updated on 19/Jul/20
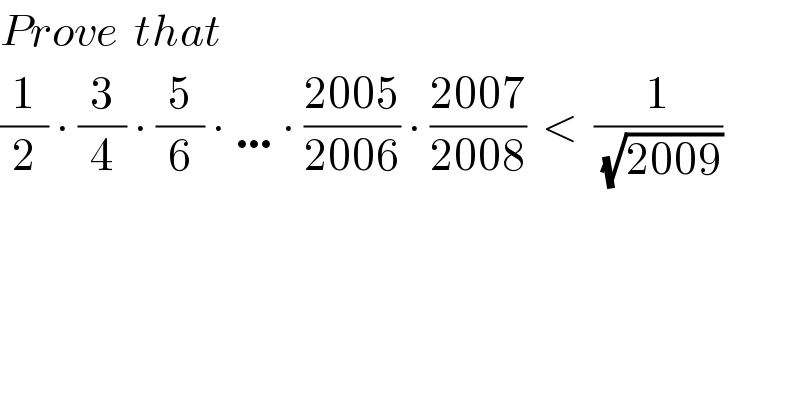
$${Prove}\:\:{that}\:\: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:\centerdot\:\frac{\mathrm{3}}{\mathrm{4}}\:\centerdot\:\frac{\mathrm{5}}{\mathrm{6}}\:\centerdot\:\ldots\centerdot\:\frac{\mathrm{2005}}{\mathrm{2006}}\:\centerdot\:\frac{\mathrm{2007}}{\mathrm{2008}}\:\:<\:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2009}}} \\ $$
Commented by JDamian last updated on 19/Jul/20
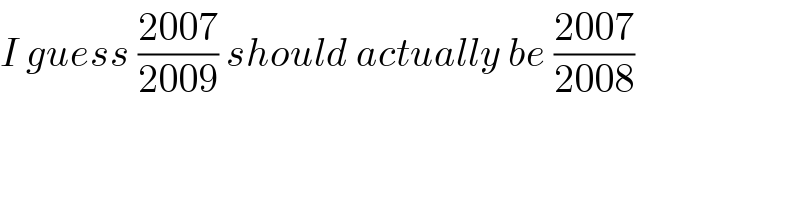
$${I}\:{guess}\:\frac{\mathrm{2007}}{\mathrm{2009}}\:{should}\:{actually}\:{be}\:\frac{\mathrm{2007}}{\mathrm{2008}} \\ $$
Answered by 1549442205PVT last updated on 19/Jul/20

$$\mathrm{It}\:\mathrm{is}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:\mathrm{that}\:\mathrm{if}\:\:\frac{\mathrm{a}}{\mathrm{b}}<\mathrm{1}\:\mathrm{then}\:\mathrm{a}<\mathrm{b} \\ $$$$\Rightarrow\mathrm{ab}+\mathrm{a}<\mathrm{ab}+\mathrm{b}\Rightarrow\mathrm{a}\left(\mathrm{b}+\mathrm{1}\right)<\mathrm{b}\left(\mathrm{a}+\mathrm{1}\right)\Rightarrow\frac{\mathrm{a}}{\mathrm{b}}<\frac{\mathrm{a}+\mathrm{1}}{\mathrm{b}+\mathrm{1}}. \\ $$$$\mathrm{Hence}, \\ $$$$\mathrm{Putting}\:\mathrm{A}=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{3}}{\mathrm{4}}.\frac{\mathrm{5}}{\mathrm{6}}….\frac{\mathrm{2005}}{\mathrm{2006}}.\frac{\mathrm{2007}}{\mathrm{2009}}.\mathrm{We}\:\mathrm{have}: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}<\frac{\mathrm{2}}{\mathrm{3}},\frac{\mathrm{3}}{\mathrm{4}}<\frac{\mathrm{4}}{\mathrm{5}},\frac{\mathrm{5}}{\mathrm{6}}<\frac{\mathrm{6}}{\mathrm{7}}…,\frac{\mathrm{2005}}{\mathrm{2006}}<\frac{\mathrm{2006}}{\mathrm{2007}},\frac{\mathrm{2007}}{\mathrm{2009}}<\frac{\mathrm{2009}}{\mathrm{2010}} \\ $$$$\mathrm{Multiplying}\:\mathrm{1004}\:\mathrm{inequlities}\:\mathrm{side}\:\mathrm{by} \\ $$$$\mathrm{side}\:\mathrm{we}\:\mathrm{getA}<\frac{\mathrm{2}}{\mathrm{3}}.\frac{\mathrm{4}}{\mathrm{5}}.\frac{\mathrm{6}}{\mathrm{7}}….\frac{\mathrm{2006}}{\mathrm{2007}}.\frac{\mathrm{2009}}{\mathrm{2010}}=\mathrm{B} \\ $$$$\Rightarrow\mathrm{A}^{\mathrm{2}} <\mathrm{AB}=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{2}}{\mathrm{3}}.\frac{\mathrm{3}}{\mathrm{4}}.\frac{\mathrm{4}}{\mathrm{5}}.\frac{\mathrm{5}}{\mathrm{6}}….\frac{\mathrm{2005}}{\mathrm{2006}}.\frac{\mathrm{2006}}{\mathrm{2007}}.\frac{\mathrm{2007}}{\mathrm{2009}}.\frac{\mathrm{2009}}{\mathrm{2010}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2010}}\Rightarrow\mathrm{A}<\frac{\mathrm{1}}{\:\sqrt{\mathrm{2010}}}<\frac{\mathrm{1}}{\:\sqrt{\mathrm{2009}}}\left(\mathrm{q}.\mathrm{e}.\mathrm{d}\right) \\ $$$$ \\ $$
