Question Number 99120 by M±th+et+s last updated on 18/Jun/20
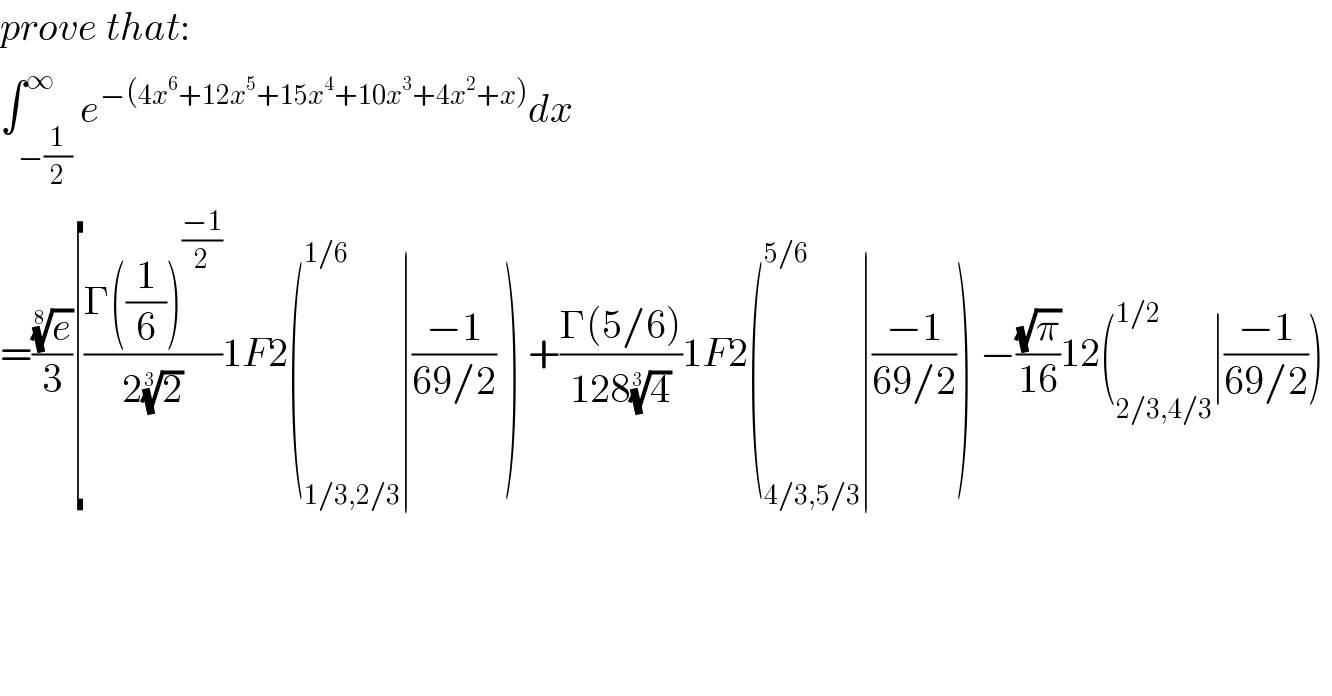
$${prove}\:{that}: \\ $$$$\int_{−\frac{\mathrm{1}}{\mathrm{2}}} ^{\infty} {e}^{−\left(\mathrm{4}{x}^{\mathrm{6}} +\mathrm{12}{x}^{\mathrm{5}} +\mathrm{15}{x}^{\mathrm{4}} +\mathrm{10}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} +{x}\right)} {dx} \\ $$$$=\frac{\sqrt[{\mathrm{8}}]{{e}}}{\mathrm{3}}\left[\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{6}}\right)^{\frac{−\mathrm{1}}{\mathrm{2}}} }{\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{2}}}\mathrm{1}{F}\mathrm{2}\left(_{\mathrm{1}/\mathrm{3},\mathrm{2}/\mathrm{3}} ^{\mathrm{1}/\mathrm{6}} \mid\frac{−\mathrm{1}}{\mathrm{69}/\mathrm{2}}\:\right)\:+\frac{\Gamma\left(\mathrm{5}/\mathrm{6}\right)}{\mathrm{128}\sqrt[{\mathrm{3}}]{\mathrm{4}}}\mathrm{1}{F}\mathrm{2}\left(_{\mathrm{4}/\mathrm{3},\mathrm{5}/\mathrm{3}} ^{\mathrm{5}/\mathrm{6}} \mid\frac{−\mathrm{1}}{\mathrm{69}/\mathrm{2}}\right)\:−\frac{\sqrt{\pi}}{\mathrm{16}}\mathrm{12}\left(_{\mathrm{2}/\mathrm{3},\mathrm{4}/\mathrm{3}} ^{\mathrm{1}/\mathrm{2}} \mid\frac{−\mathrm{1}}{\mathrm{69}/\mathrm{2}}\right)\:\right. \\ $$
Commented by M±th+et+s last updated on 18/Jun/20
![I=(((e)^(1/8) .π(√π))/(2(4)^(1/3) (3)^(1/6) ))[(Ai(((−1)/(8(6)^(1/3) ))))^2 +(Bi(((−1)/(8(6)^(1/3) ))))^2 ]](https://www.tinkutara.com/question/Q99121.png)
$${I}=\frac{\sqrt[{\mathrm{8}}]{{e}}.\pi\sqrt{\pi}}{\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{4}}\sqrt[{\mathrm{6}}]{\mathrm{3}}}\left[\left(\mathrm{Ai}\left(\frac{−\mathrm{1}}{\mathrm{8}\sqrt[{\mathrm{3}}]{\mathrm{6}}}\right)\right)^{\mathrm{2}} +\left(\mathrm{Bi}\left(\frac{−\mathrm{1}}{\mathrm{8}\sqrt[{\mathrm{3}}]{\mathrm{6}}}\right)\right)^{\mathrm{2}} \right] \\ $$
Commented by M±th+et+s last updated on 18/Jun/20

$$\mathrm{Ai}\left(\mathrm{z}\right)\::\:{Airy}\:{function} \\ $$$$\mathrm{Bi}\left(\mathrm{z}\right):\:{Airy}\:\mathrm{Bi}\:{function} \\ $$$$\mathrm{1}{F}\mathrm{2}:\:{is}\:{hyper}\:{geometric}\:{function} \\ $$$$\Gamma\left({s}\right):{gamma}\:{function} \\ $$
