Menu Close

prove-that-1-4-2pi-3-56-3-

Tinku Tara 0 Comments
Pin




Question Number 162377 by mnjuly1970 last updated on 29/Dec/21
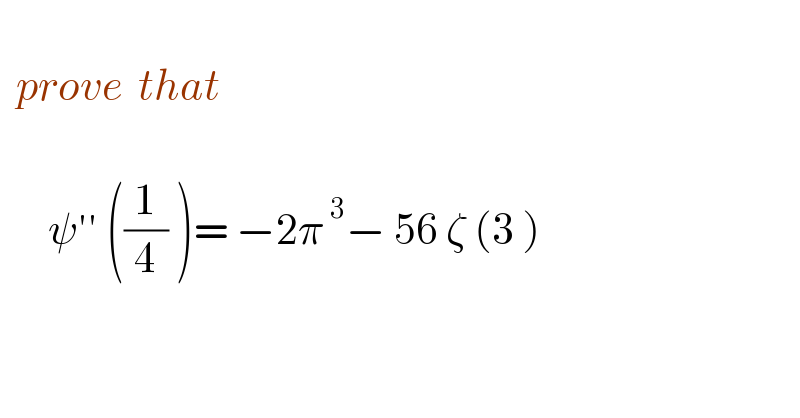
prove that ψ′′ ((1/4) )= −2π^( 3) − 56 ζ (3 )
$$ \\ $$$$\:\:{prove}\:\:{that} \\ $$$$ \\ $$$$\:\:\:\:\:\:\psi''\:\left(\frac{\mathrm{1}}{\mathrm{4}}\:\right)=\:−\mathrm{2}\pi^{\:\mathrm{3}} −\:\mathrm{56}\:\zeta\:\left(\mathrm{3}\:\right) \\ $$$$ \\ $$
Commented by aleks041103 last updated on 29/Dec/21
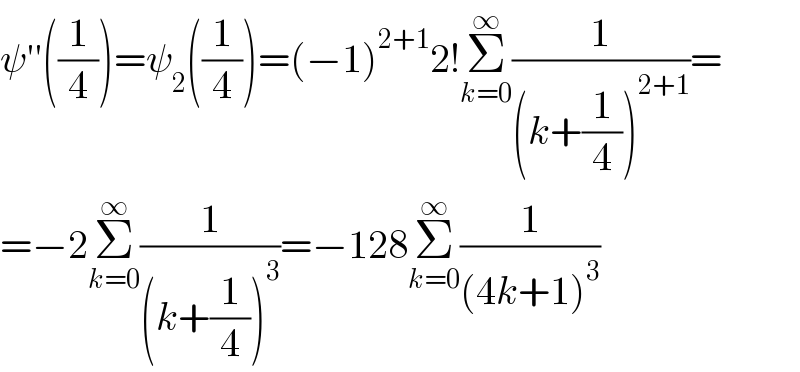
ψ′′((1/4))=ψ_2 ((1/4))=(−1)^(2+1) 2!Σ_(k=0) ^∞ (1/((k+(1/4))^(2+1) ))= =−2Σ_(k=0) ^∞ (1/((k+(1/4))^3 ))=−128Σ_(k=0) ^∞ (1/((4k+1)^3 ))
$$\psi''\left(\frac{\mathrm{1}}{\mathrm{4}}\right)=\psi_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)=\left(−\mathrm{1}\right)^{\mathrm{2}+\mathrm{1}} \mathrm{2}!\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({k}+\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}+\mathrm{1}} }= \\ $$$$=−\mathrm{2}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({k}+\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{3}} }=−\mathrm{128}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{4}{k}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$
Commented by amin96 last updated on 29/Dec/21
bravo
$${bravo} \\ $$
Answered by mindispower last updated on 30/Dec/21
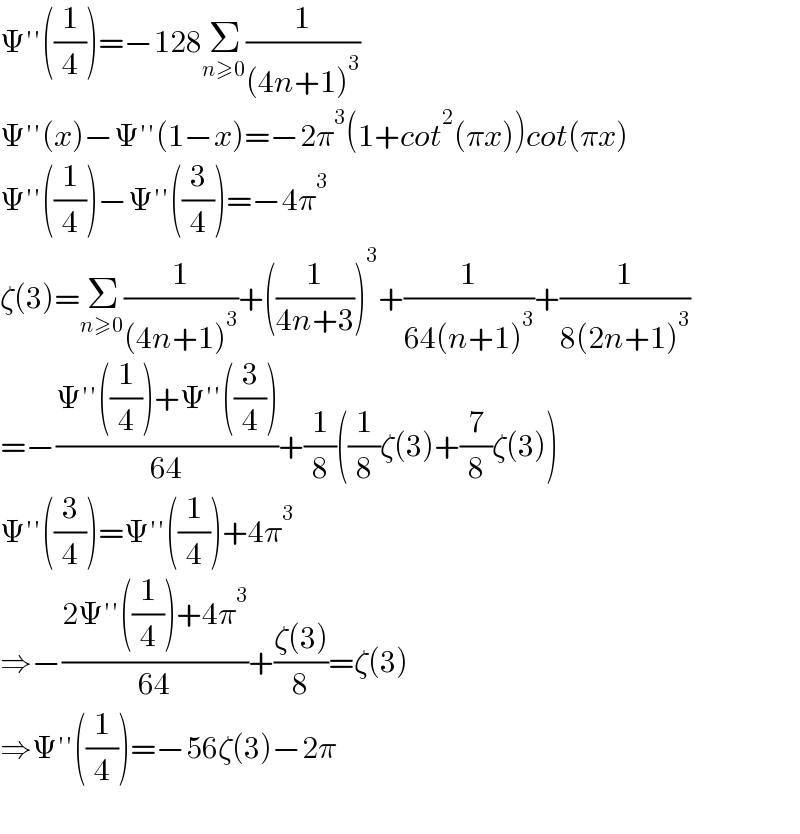
Ψ′′((1/4))=−128Σ_(n≥0) (1/((4n+1)^3 )) Ψ′′(x)−Ψ′′(1−x)=−2π^3 (1+cot^2 (πx))cot(πx) Ψ′′((1/4))−Ψ′′((3/4))=−4π^3 ζ(3)=Σ_(n≥0) (1/((4n+1)^3 ))+((1/(4n+3)))^3 +(1/(64(n+1)^3 ))+(1/(8(2n+1)^3 )) =−((Ψ′′((1/4))+Ψ′′((3/4)))/(64))+(1/8)((1/8)ζ(3)+(7/8)ζ(3)) Ψ′′((3/4))=Ψ′′((1/4))+4π^3 ⇒−((2Ψ′′((1/4))+4π^3 )/(64))+((ζ(3))/8)=ζ(3) ⇒Ψ′′((1/4))=−56ζ(3)−2π
$$\Psi''\left(\frac{\mathrm{1}}{\mathrm{4}}\right)=−\mathrm{128}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{4}{n}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\Psi''\left({x}\right)−\Psi''\left(\mathrm{1}−{x}\right)=−\mathrm{2}\pi^{\mathrm{3}} \left(\mathrm{1}+{cot}^{\mathrm{2}} \left(\pi{x}\right)\right){cot}\left(\pi{x}\right) \\ $$$$\Psi''\left(\frac{\mathrm{1}}{\mathrm{4}}\right)−\Psi''\left(\frac{\mathrm{3}}{\mathrm{4}}\right)=−\mathrm{4}\pi^{\mathrm{3}} \\ $$$$\zeta\left(\mathrm{3}\right)=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{4}{n}+\mathrm{1}\right)^{\mathrm{3}} }+\left(\frac{\mathrm{1}}{\mathrm{4}{n}+\mathrm{3}}\right)^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{64}\left({n}+\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{8}\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=−\frac{\Psi''\left(\frac{\mathrm{1}}{\mathrm{4}}\right)+\Psi''\left(\frac{\mathrm{3}}{\mathrm{4}}\right)}{\mathrm{64}}+\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{1}}{\mathrm{8}}\zeta\left(\mathrm{3}\right)+\frac{\mathrm{7}}{\mathrm{8}}\zeta\left(\mathrm{3}\right)\right) \\ $$$$\Psi''\left(\frac{\mathrm{3}}{\mathrm{4}}\right)=\Psi''\left(\frac{\mathrm{1}}{\mathrm{4}}\right)+\mathrm{4}\pi^{\mathrm{3}} \\ $$$$\Rightarrow−\frac{\mathrm{2}\Psi''\left(\frac{\mathrm{1}}{\mathrm{4}}\right)+\mathrm{4}\pi^{\mathrm{3}} }{\mathrm{64}}+\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{8}}=\zeta\left(\mathrm{3}\right) \\ $$$$\Rightarrow\Psi''\left(\frac{\mathrm{1}}{\mathrm{4}}\right)=−\mathrm{56}\zeta\left(\mathrm{3}\right)−\mathrm{2}\pi \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *