Question Number 181722 by Agnibhoo98 last updated on 29/Nov/22
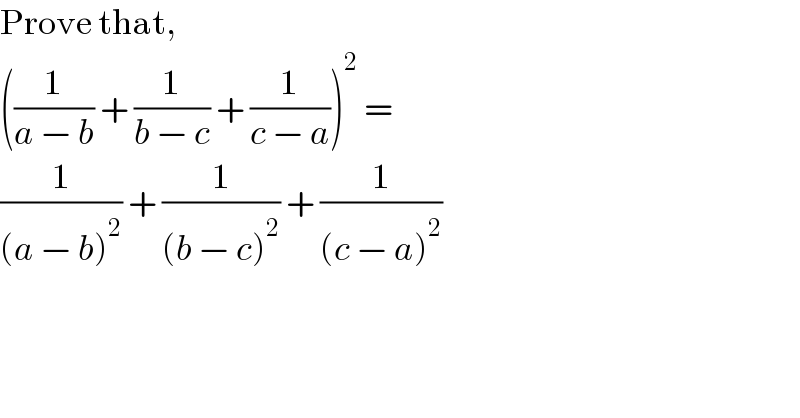
$$\mathrm{Prove}\:\mathrm{that}, \\ $$$$\left(\frac{\mathrm{1}}{{a}\:−\:{b}}\:+\:\frac{\mathrm{1}}{{b}\:−\:{c}}\:+\:\frac{\mathrm{1}}{{c}\:−\:{a}}\right)^{\mathrm{2}} \:=\: \\ $$$$\frac{\mathrm{1}}{\left({a}\:−\:{b}\right)^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\left({b}\:−\:{c}\right)^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\left({c}\:−\:{a}\right)^{\mathrm{2}} } \\ $$
Answered by Rasheed.Sindhi last updated on 29/Nov/22

$$\left(\frac{\mathrm{1}}{{a}\:−\:{b}}\:+\:\frac{\mathrm{1}}{{b}\:−\:{c}}\:+\:\frac{\mathrm{1}}{{c}\:−\:{a}}\right)^{\mathrm{2}} \:=\: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\left({a}\:−\:{b}\right)^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\left({b}\:−\:{c}\right)^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\left({c}\:−\:{a}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$${a}−{b}={p}\:,\:{b}−{c}={q}\:,\:{c}−{a}={r} \\ $$$${p}+{q}+{r}=\mathrm{0} \\ $$$$\mathcal{T}{o}\:{prove}: \\ $$$$\left(\frac{\mathrm{1}}{{p}}+\frac{\mathrm{1}}{{q}}+\frac{\mathrm{1}}{{r}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{{p}^{\mathrm{2}} }+\frac{\mathrm{1}}{{q}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}^{\mathrm{2}} } \\ $$$$\mathrm{LHS}: \\ $$$$\frac{\mathrm{1}}{{p}^{\mathrm{2}} }+\frac{\mathrm{1}}{{q}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }+\mathrm{2}\left(\frac{\mathrm{1}}{{pq}}+\frac{\mathrm{1}}{{qr}}+\frac{\mathrm{1}}{{rp}}\right) \\ $$$$ \\ $$$$\frac{\mathrm{1}}{{p}^{\mathrm{2}} }+\frac{\mathrm{1}}{{q}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }+\mathrm{2}\left(\frac{{r}}{{pqr}}+\frac{{p}}{{pqr}}+\frac{{q}}{{pqr}}\right) \\ $$$$\frac{\mathrm{1}}{{p}^{\mathrm{2}} }+\frac{\mathrm{1}}{{q}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }+\mathrm{2}\left(\frac{{p}+{q}+{r}}{{pqr}}\right) \\ $$$$\frac{\mathrm{1}}{{p}^{\mathrm{2}} }+\frac{\mathrm{1}}{{q}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }+\mathrm{2}\left(\frac{\mathrm{0}}{{pqr}}\right) \\ $$$$\frac{\mathrm{1}}{{p}^{\mathrm{2}} }+\frac{\mathrm{1}}{{q}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }=\mathrm{RHS} \\ $$
