Question Number 19291 by Tinkutara last updated on 08/Aug/17
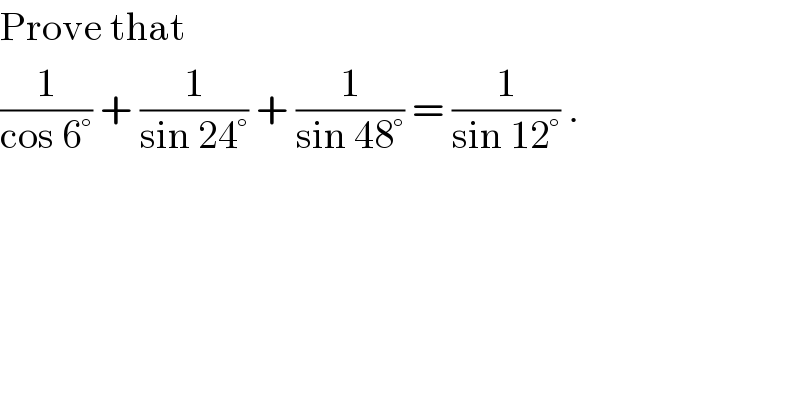
$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{6}°}\:+\:\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{24}°}\:+\:\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{48}°}\:=\:\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{12}°}\:. \\ $$
Answered by Tinkutara last updated on 16/Aug/17
![(1/(cos 6°)) − (1/(sin 12°)) + (1/(sin 24°)) + (1/(sin 48°)) = (1/(cos 6°)) − (1/(sin 12°)) + ((sin 48° + sin 24°)/(sin 48° sin 24°)) = (1/(cos 6°)) − (1/(sin 12°)) + ((sin 36°)/(sin 48° sin 12°)) = (1/(cos 6°)) − (1/(sin 12°))(((sin 48° − sin 36°)/(sin 48°))) = (1/(cos 6°)) − (1/(sin 12°))(((2 cos 42° sin 6°)/(sin 48°))) = (1/(cos 6°)) − ((2 sin 6°)/(2 sin 6° cos 6°)) [∵ cos 42° = sin 48°] = (1/(cos 6°)) − (1/(cos 6°)) = 0](https://www.tinkutara.com/question/Q19854.png)
$$\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{6}°}\:−\:\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{12}°}\:+\:\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{24}°}\:+\:\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{48}°} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{6}°}\:−\:\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{12}°}\:+\:\frac{\mathrm{sin}\:\mathrm{48}°\:+\:\mathrm{sin}\:\mathrm{24}°}{\mathrm{sin}\:\mathrm{48}°\:\mathrm{sin}\:\mathrm{24}°} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{6}°}\:−\:\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{12}°}\:+\:\frac{\mathrm{sin}\:\mathrm{36}°}{\mathrm{sin}\:\mathrm{48}°\:\mathrm{sin}\:\mathrm{12}°} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{6}°}\:−\:\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{12}°}\left(\frac{\mathrm{sin}\:\mathrm{48}°\:−\:\mathrm{sin}\:\mathrm{36}°}{\mathrm{sin}\:\mathrm{48}°}\right) \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{6}°}\:−\:\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{12}°}\left(\frac{\mathrm{2}\:\mathrm{cos}\:\mathrm{42}°\:\mathrm{sin}\:\mathrm{6}°}{\mathrm{sin}\:\mathrm{48}°}\right) \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{6}°}\:−\:\frac{\mathrm{2}\:\mathrm{sin}\:\mathrm{6}°}{\mathrm{2}\:\mathrm{sin}\:\mathrm{6}°\:\mathrm{cos}\:\mathrm{6}°}\:\left[\because\:\mathrm{cos}\:\mathrm{42}°\:=\:\mathrm{sin}\:\mathrm{48}°\right] \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{6}°}\:−\:\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{6}°}\:=\:\mathrm{0} \\ $$
