Menu Close

prove-that-1-I-0-pi-2-sin-x-tan-x-sin-x-dx-pi-2-2-J-0-pi-2-sin-x-tan-x-sin-x-dx-1-e-1-2-pi-

Tinku Tara 0 Comments
Pin




Question Number 158590 by mnjuly1970 last updated on 06/Nov/21
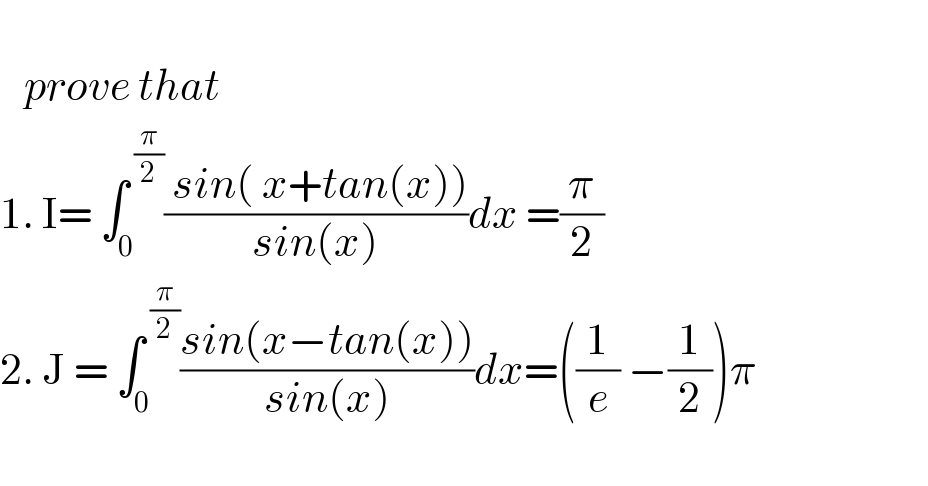
prove that 1. I= ∫_0 ^( (π/2)) (( sin( x+tan(x)))/(sin(x)))dx =(π/2) 2. J = ∫_0 ^( (π/2)) ((sin(x−tan(x)))/(sin(x)))dx=((1/e) −(1/2))π
$$ \\ $$$$\:\:\:{prove}\:{that}\: \\ $$$$\mathrm{1}.\:\mathrm{I}=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{\:{sin}\left(\:{x}+{tan}\left({x}\right)\right)}{{sin}\left({x}\right)}{dx}\:=\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{2}.\:\mathrm{J}\:=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{{sin}\left({x}−{tan}\left({x}\right)\right)}{{sin}\left({x}\right)}{dx}=\left(\frac{\mathrm{1}}{{e}}\:−\frac{\mathrm{1}}{\mathrm{2}}\right)\pi \\ $$$$ \\ $$
Answered by qaz last updated on 06/Nov/21
I=∫_0 ^(π/2) ((sin x∙cos (tan x)+cos x∙sin (tan x))/(sin x))dx =∫_0 ^(π/2) cos (tan x)+((sin (tan x))/(tan x))dx............tan x→x =∫_0 ^∞ (cos x+((sin x)/x))(dx/(1+x^2 )) =∫_0 ^∞ ((cos x)/(1+x^2 ))+((1/x)−(x/(1+x^2 )))sin xdx =∫_0 ^∞ L{cos x}∙L^(−1) {(1/(1+x^2 ))}+((1/x)−(x/(1+x^2 )))sin xdx =∫_0 ^∞ (x/(1+x^2 ))∙sin x+((1/x)−(x/(1+x^2 )))∙sin xdx =(π/2) −−−−−−−−−−−−−−− J=∫_0 ^(π/2) ((sin (x−tan x))/(sin x))dx =∫_0 ^(π/2) ((sin x∙cos (tan x)−cos x∙sin (tan x))/(sin x))dx =∫_0 ^(π/2) cos (tan x)−((sin (tan x))/(tan x))dx.........tan x→x =∫_0 ^∞ (cos x−((sin x)/x))(dx/(1+x^2 )) =∫_0 ^∞ (((2cos x)/(1+x^2 ))−((sin x)/x))dx =(π/e)−(π/2) −−−−−−−−−−− ∫_0 ^∞ ((sin x)/x)dx=∫_0 ^∞ L{sin x}∙L^(−1) {(1/x)}dx =∫_0 ^∞ (1/(1+x^2 ))∙1dx=(π/2) −−−−−−−−−−−− ∫_0 ^∞ ((L{cos tx})/(1+x^2 ))dx=∫_0 ^∞ (s/((s^2 +x^2 )(1+x^2 )))dx=(π/(2(1+s))) ⇒∫_0 ^∞ ((cos x)/(1+x^2 ))dx=L^(−1) {(π/(2(1+s)))}_(t=1) =(π/2)e^(−1)
$$\mathrm{I}=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\mathrm{sin}\:\mathrm{x}\centerdot\mathrm{cos}\:\left(\mathrm{tan}\:\mathrm{x}\right)+\mathrm{cos}\:\mathrm{x}\centerdot\mathrm{sin}\:\left(\mathrm{tan}\:\mathrm{x}\right)}{\mathrm{sin}\:\mathrm{x}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{cos}\:\left(\mathrm{tan}\:\mathrm{x}\right)+\frac{\mathrm{sin}\:\left(\mathrm{tan}\:\mathrm{x}\right)}{\mathrm{tan}\:\mathrm{x}}\mathrm{dx}…………\mathrm{tan}\:\mathrm{x}\rightarrow\mathrm{x} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\mathrm{cos}\:\mathrm{x}+\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\right)\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{cos}\:\mathrm{x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }+\left(\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\mathrm{sin}\:\mathrm{xdx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \mathscr{L}\left\{\mathrm{cos}\:\mathrm{x}\right\}\centerdot\mathscr{L}^{−\mathrm{1}} \left\{\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right\}+\left(\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\mathrm{sin}\:\mathrm{xdx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\centerdot\mathrm{sin}\:\mathrm{x}+\left(\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\centerdot\mathrm{sin}\:\mathrm{xdx} \\ $$$$=\frac{\pi}{\mathrm{2}} \\ $$$$−−−−−−−−−−−−−−− \\ $$$$\mathrm{J}=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\mathrm{sin}\:\left(\mathrm{x}−\mathrm{tan}\:\mathrm{x}\right)}{\mathrm{sin}\:\mathrm{x}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\mathrm{sin}\:\mathrm{x}\centerdot\mathrm{cos}\:\left(\mathrm{tan}\:\mathrm{x}\right)−\mathrm{cos}\:\mathrm{x}\centerdot\mathrm{sin}\:\left(\mathrm{tan}\:\mathrm{x}\right)}{\mathrm{sin}\:\mathrm{x}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{cos}\:\left(\mathrm{tan}\:\mathrm{x}\right)−\frac{\mathrm{sin}\:\left(\mathrm{tan}\:\mathrm{x}\right)}{\mathrm{tan}\:\mathrm{x}}\mathrm{dx}………\mathrm{tan}\:\mathrm{x}\rightarrow\mathrm{x} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\mathrm{cos}\:\mathrm{x}−\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\right)\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{2cos}\:\mathrm{x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\right)\mathrm{dx} \\ $$$$=\frac{\pi}{\mathrm{e}}−\frac{\pi}{\mathrm{2}} \\ $$$$−−−−−−−−−−− \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\mathrm{dx}=\int_{\mathrm{0}} ^{\infty} \mathscr{L}\left\{\mathrm{sin}\:\mathrm{x}\right\}\centerdot\mathscr{L}^{−\mathrm{1}} \left\{\frac{\mathrm{1}}{\mathrm{x}}\right\}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\centerdot\mathrm{1dx}=\frac{\pi}{\mathrm{2}} \\ $$$$−−−−−−−−−−−− \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathscr{L}\left\{\mathrm{cos}\:\mathrm{tx}\right\}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{s}}{\left(\mathrm{s}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\mathrm{dx}=\frac{\pi}{\mathrm{2}\left(\mathrm{1}+\mathrm{s}\right)} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{cos}\:\mathrm{x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}=\mathscr{L}^{−\mathrm{1}} \left\{\frac{\pi}{\mathrm{2}\left(\mathrm{1}+\mathrm{s}\right)}\right\}_{\mathrm{t}=\mathrm{1}} =\frac{\pi}{\mathrm{2}}\mathrm{e}^{−\mathrm{1}} \\ $$
Commented by puissant last updated on 06/Nov/21
Ω=∫_0 ^∞ ((cosx)/(x^2 +1))dx = (1/2)∫_(−∞) ^(+∞) ((cosx)/(x^2 +1))dx = (1/2)Re(∫_(−∞) ^(+∞) (e^(ix) /(x^2 +1))dx) = (1/2)(2iπ•res((e^(ix) /(x^2 +1)),+i)) Ω = iπ•lim_(x→+i) ((e^(iπ) /(x+i)))=iπ×(e^(−1) /(2i)) = (π/(2e)).. Ω = ∫_0 ^∞ ((cosx)/(x^2 +1)) dx = (π/(2e)).. ............Le puissant............
$$\Omega=\int_{\mathrm{0}} ^{\infty} \frac{{cosx}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \frac{{cosx}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}{Re}\left(\int_{−\infty} ^{+\infty} \frac{{e}^{{ix}} }{{x}^{\mathrm{2}} +\mathrm{1}}{dx}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{i}\pi\bullet{res}\left(\frac{{e}^{{ix}} }{{x}^{\mathrm{2}} +\mathrm{1}},+{i}\right)\right) \\ $$$$\Omega\:=\:{i}\pi\bullet\underset{{x}\rightarrow+{i}} {\mathrm{lim}}\left(\frac{{e}^{{i}\pi} }{{x}+{i}}\right)={i}\pi×\frac{{e}^{−\mathrm{1}} }{\mathrm{2}{i}}\:=\:\frac{\pi}{\mathrm{2}{e}}.. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Omega\:=\:\int_{\mathrm{0}} ^{\infty} \frac{{cosx}}{{x}^{\mathrm{2}} +\mathrm{1}}\:{dx}\:=\:\frac{\pi}{\mathrm{2}{e}}.. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…………\mathscr{L}{e}\:{puissant}………… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *