Question Number 164533 by alephzero last updated on 18/Jan/22
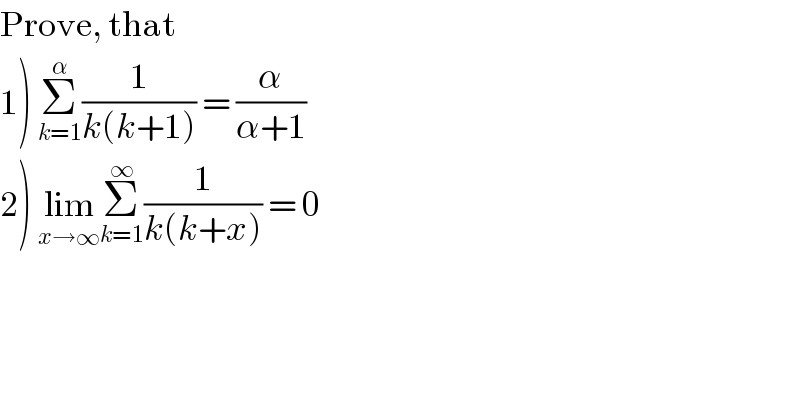
$$\mathrm{Prove},\:\mathrm{that} \\ $$$$\left.\mathrm{1}\right)\:\underset{{k}=\mathrm{1}} {\overset{\alpha} {\sum}}\frac{\mathrm{1}}{{k}\left({k}+\mathrm{1}\right)}\:=\:\frac{\alpha}{\alpha+\mathrm{1}} \\ $$$$\left.\mathrm{2}\right)\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}\left({k}+{x}\right)}\:=\:\mathrm{0} \\ $$
Answered by amin96 last updated on 18/Jan/22
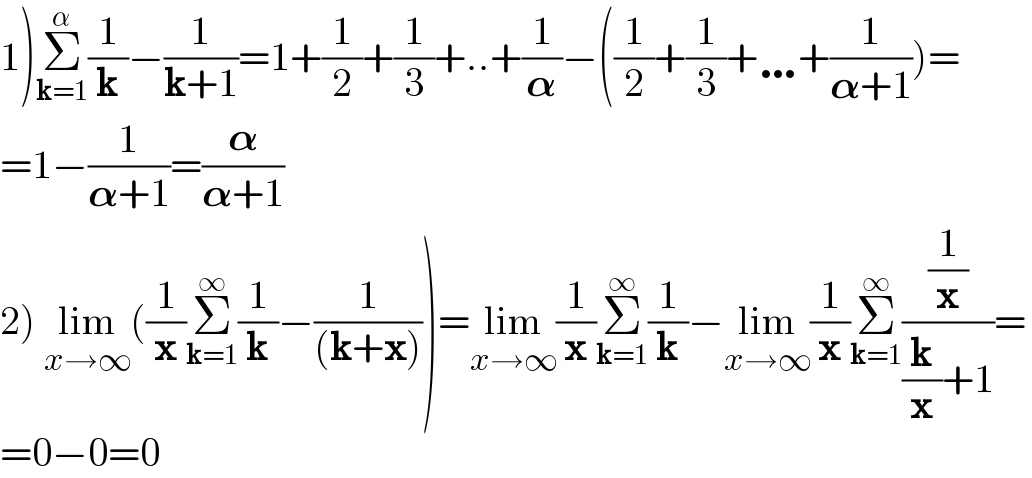
$$\left.\mathrm{1}\right)\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\alpha} {\sum}}\frac{\mathrm{1}}{\boldsymbol{\mathrm{k}}}−\frac{\mathrm{1}}{\boldsymbol{\mathrm{k}}+\mathrm{1}}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+..+\frac{\mathrm{1}}{\boldsymbol{\alpha}}−\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\ldots+\frac{\mathrm{1}}{\boldsymbol{\alpha}+\mathrm{1}}\right)= \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\boldsymbol{\alpha}+\mathrm{1}}=\frac{\boldsymbol{\alpha}}{\boldsymbol{\alpha}+\mathrm{1}} \\ $$$$\left.\mathrm{2}\right)\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\boldsymbol{\mathrm{k}}}−\frac{\mathrm{1}}{\left(\boldsymbol{\mathrm{k}}+\boldsymbol{\mathrm{x}}\right)}\right)=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\boldsymbol{\mathrm{k}}}−\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}}{\frac{\boldsymbol{\mathrm{k}}}{\boldsymbol{\mathrm{x}}}+\mathrm{1}}= \\ $$$$=\mathrm{0}−\mathrm{0}=\mathrm{0} \\ $$
Commented by alephzero last updated on 18/Jan/22

$$\mathrm{Thank}\:\mathrm{You},\:\mathrm{sir} \\ $$
Answered by Rasheed.Sindhi last updated on 18/Jan/22
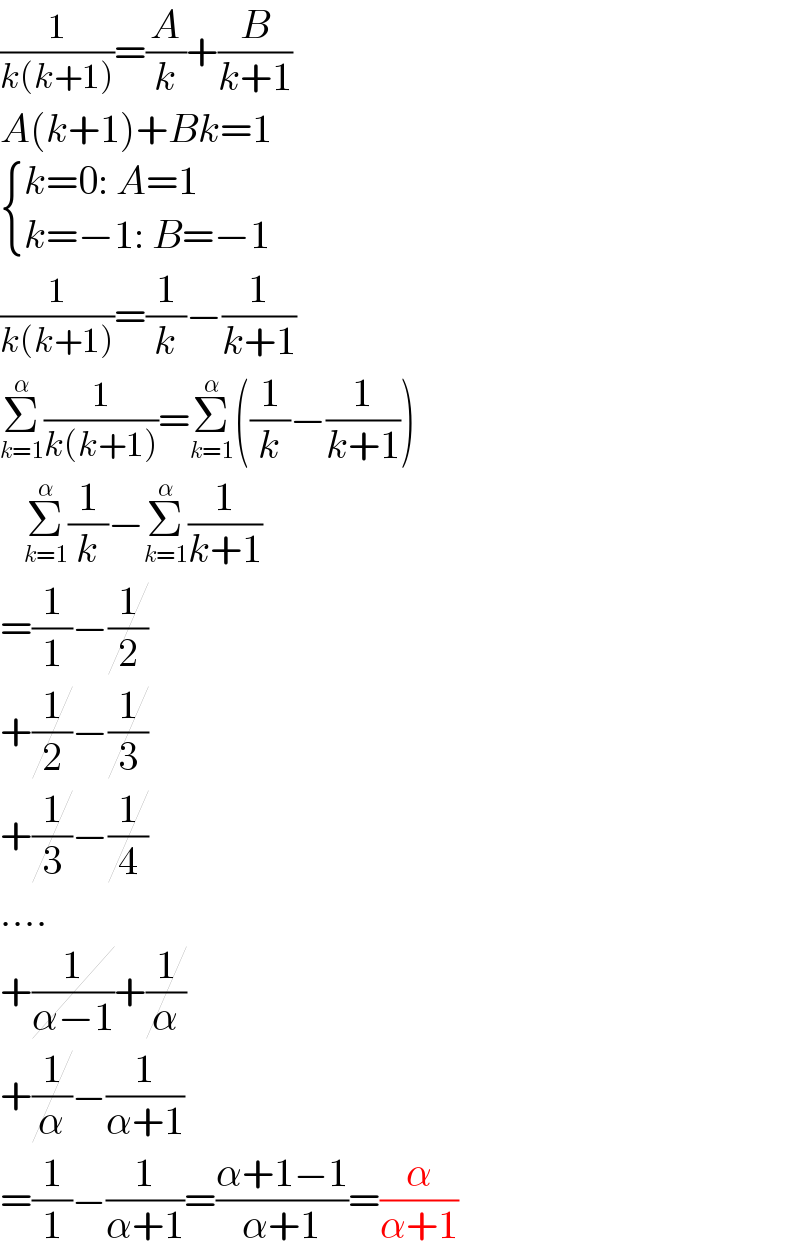
$$\frac{\mathrm{1}}{{k}\left({k}+\mathrm{1}\right)}=\frac{{A}}{{k}}+\frac{{B}}{{k}+\mathrm{1}} \\ $$$${A}\left({k}+\mathrm{1}\right)+{Bk}=\mathrm{1} \\ $$$$\begin{cases}{{k}=\mathrm{0}:\:{A}=\mathrm{1}}\\{{k}=−\mathrm{1}:\:{B}=−\mathrm{1}}\end{cases} \\ $$$$\frac{\mathrm{1}}{{k}\left({k}+\mathrm{1}\right)}=\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{{k}+\mathrm{1}} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\alpha} {\sum}}\frac{\mathrm{1}}{{k}\left({k}+\mathrm{1}\right)}=\underset{{k}=\mathrm{1}} {\overset{\alpha} {\sum}}\left(\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{{k}+\mathrm{1}}\right) \\ $$$$\:\:\:\underset{{k}=\mathrm{1}} {\overset{\alpha} {\sum}}\frac{\mathrm{1}}{{k}}−\underset{{k}=\mathrm{1}} {\overset{\alpha} {\sum}}\frac{\mathrm{1}}{{k}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}}−\cancel{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$+\cancel{\frac{\mathrm{1}}{\mathrm{2}}}−\cancel{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$+\cancel{\frac{\mathrm{1}}{\mathrm{3}}}−\cancel{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$…. \\ $$$$+\cancel{\frac{\mathrm{1}}{\alpha−\mathrm{1}}}+\cancel{\frac{\mathrm{1}}{\alpha}} \\ $$$$+\cancel{\frac{\mathrm{1}}{\alpha}}−\frac{\mathrm{1}}{\alpha+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}}−\frac{\mathrm{1}}{\alpha+\mathrm{1}}=\frac{\alpha+\mathrm{1}−\mathrm{1}}{\alpha+\mathrm{1}}=\frac{\alpha}{\alpha+\mathrm{1}} \\ $$
Commented by alephzero last updated on 18/Jan/22

$$\mathrm{Thank}\:\mathrm{You}\:\mathrm{sir}. \\ $$
