Question Number 23357 by Tinkutara last updated on 29/Oct/17
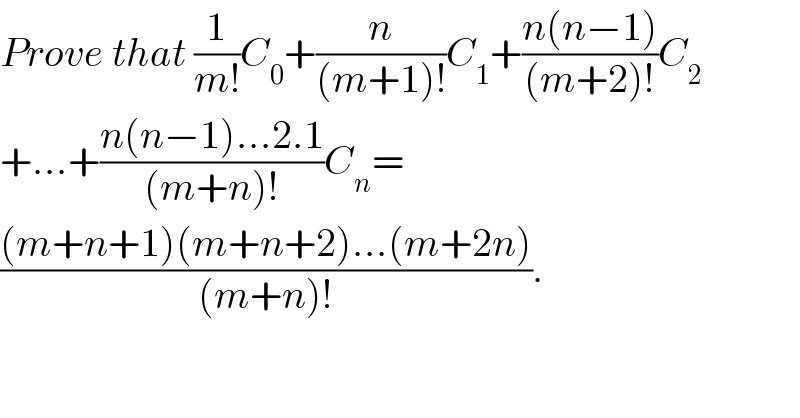
$${Prove}\:{that}\:\frac{\mathrm{1}}{{m}!}{C}_{\mathrm{0}} +\frac{{n}}{\left({m}+\mathrm{1}\right)!}{C}_{\mathrm{1}} +\frac{{n}\left({n}−\mathrm{1}\right)}{\left({m}+\mathrm{2}\right)!}{C}_{\mathrm{2}} \\ $$$$+…+\frac{{n}\left({n}−\mathrm{1}\right)…\mathrm{2}.\mathrm{1}}{\left({m}+{n}\right)!}{C}_{{n}} = \\ $$$$\frac{\left({m}+{n}+\mathrm{1}\right)\left({m}+{n}+\mathrm{2}\right)…\left({m}+\mathrm{2}{n}\right)}{\left({m}+{n}\right)!}. \\ $$
