Question Number 128788 by bramlexs22 last updated on 10/Jan/21
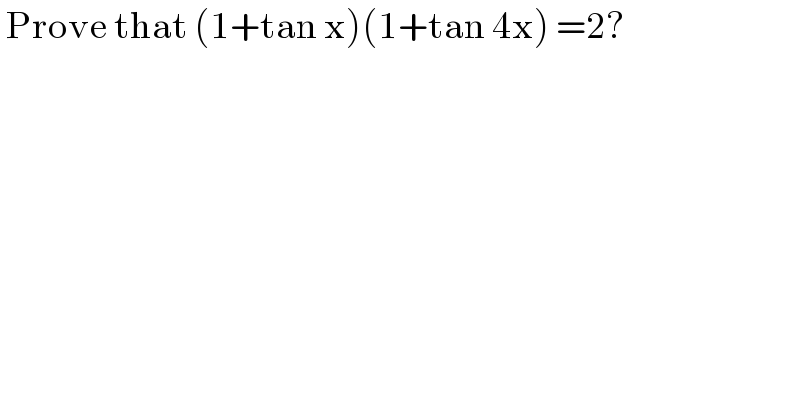
$$\:\mathrm{Prove}\:\mathrm{that}\:\left(\mathrm{1}+\mathrm{tan}\:\mathrm{x}\right)\left(\mathrm{1}+\mathrm{tan}\:\mathrm{4x}\right)\:=\mathrm{2}? \\ $$
Commented by bramlexs22 last updated on 10/Jan/21
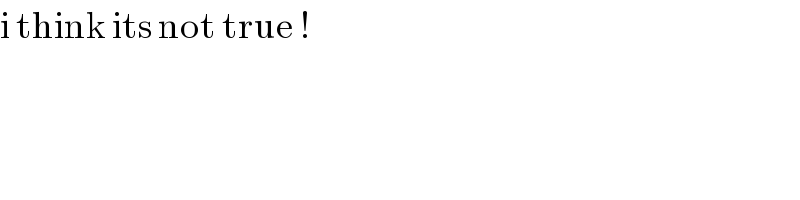
$$\mathrm{i}\:\mathrm{think}\:\mathrm{its}\:\mathrm{not}\:\mathrm{true}\:! \\ $$
Commented by mr W last updated on 10/Jan/21

$${it}\:\boldsymbol{{is}}\:{not}\:{true}! \\ $$
Commented by liberty last updated on 10/Jan/21
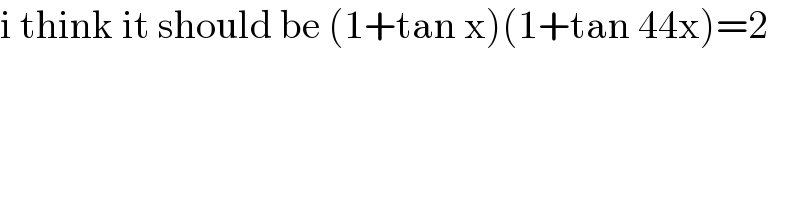
$$\mathrm{i}\:\mathrm{think}\:\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\left(\mathrm{1}+\mathrm{tan}\:\mathrm{x}\right)\left(\mathrm{1}+\mathrm{tan}\:\mathrm{44x}\right)=\mathrm{2} \\ $$
Commented by mr W last updated on 10/Jan/21
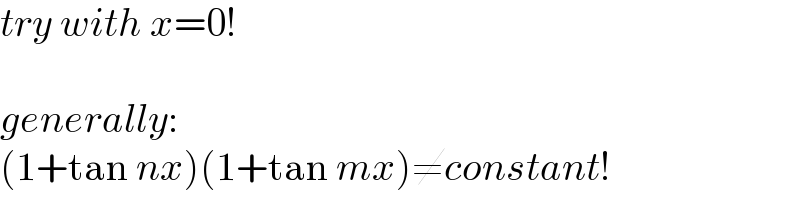
$${try}\:{with}\:{x}=\mathrm{0}! \\ $$$$ \\ $$$${generally}: \\ $$$$\left(\mathrm{1}+\mathrm{tan}\:{nx}\right)\left(\mathrm{1}+\mathrm{tan}\:{mx}\right)\neq{constant}! \\ $$
Commented by liberty last updated on 10/Jan/21

$$\mathrm{for}\:\mathrm{nx}+\mathrm{mx}\:=\:\frac{\pi}{\mathrm{4}}\:\mathrm{it}\:\mathrm{is}\:\mathrm{true}! \\ $$
Commented by liberty last updated on 10/Jan/21
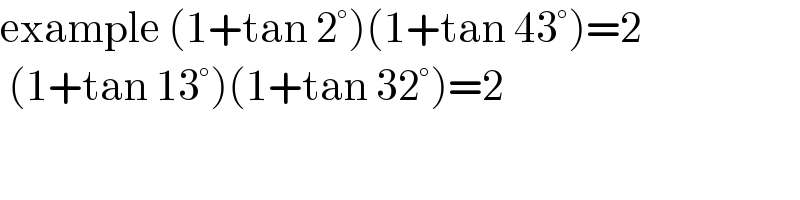
$$\mathrm{example}\:\left(\mathrm{1}+\mathrm{tan}\:\mathrm{2}°\right)\left(\mathrm{1}+\mathrm{tan}\:\mathrm{43}°\right)=\mathrm{2} \\ $$$$\:\left(\mathrm{1}+\mathrm{tan}\:\mathrm{13}°\right)\left(\mathrm{1}+\mathrm{tan}\:\mathrm{32}°\right)=\mathrm{2} \\ $$
Commented by mr W last updated on 10/Jan/21
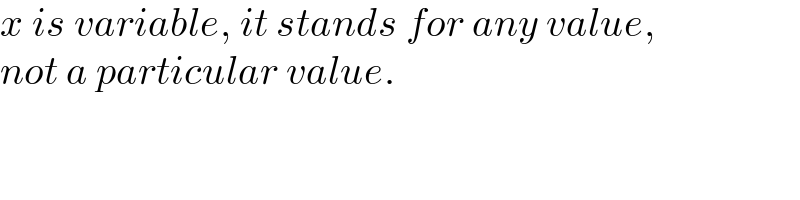
$${x}\:{is}\:{variable},\:{it}\:{stands}\:{for}\:{any}\:{value}, \\ $$$${not}\:{a}\:{particular}\:{value}. \\ $$
Commented by benjo_mathlover last updated on 10/Jan/21
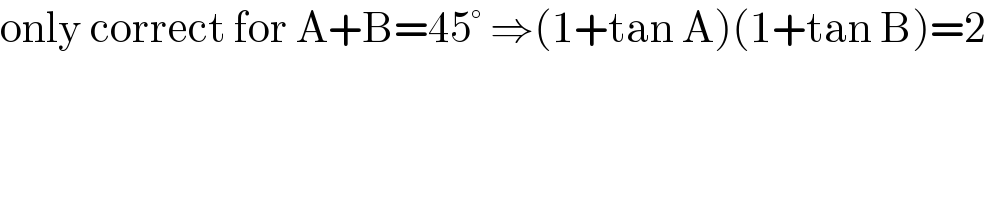
$$\mathrm{only}\:\mathrm{correct}\:\mathrm{for}\:\mathrm{A}+\mathrm{B}=\mathrm{45}°\:\Rightarrow\left(\mathrm{1}+\mathrm{tan}\:\mathrm{A}\right)\left(\mathrm{1}+\mathrm{tan}\:\mathrm{B}\right)=\mathrm{2} \\ $$$$ \\ $$
Answered by Olaf last updated on 10/Jan/21
![f(x) = (1+tanx)(1+tan4x) f(x) = (((cosx+sinx)(cos4x+sin4x))/(cosxcos4x)) f(x) = ((cosxcos4x+sinxsin4x+sinxcos4x+cosxsin4x)/(cosxcos4x)) f(x) = ((cos3x+sin5x)/(cosxcos4x)) f(x) = ((cos3x+cos((π/2)−5x))/(cosxcos4x)) f(x) = ((2cos(((3x+(π/2)−5x)/2))cos(((3x−(π/2)+5x)/2)))/(cosxcos4x)) f(x) = ((2cos(x−(π/4))cos(4x−(π/4)))/(cosxcos4x)) f(x) = 2 ⇔ cos(x−(π/4))cos(4x−(π/4)) = cosxcos4x ⇔ (1/2)[cos3x+cos(5x−(π/2))] = (1/2)[cos3x+cos5x] ⇔ cos(5x−(π/2)) = cos5x ⇔ 5x−(π/2) = ±5x+2kπ, k∈Z ⇔ x = (π/(20)) +((kπ)/(10)), k∈Z S = {(π/(20))+((kπ)/(10)), k∈Z} Numerically we can verify for example that, for k = 0 : (1+tan(π/(20)))(1+tan(π/5)) = 2](https://www.tinkutara.com/question/Q128804.png)
$${f}\left({x}\right)\:=\:\left(\mathrm{1}+\mathrm{tan}{x}\right)\left(\mathrm{1}+\mathrm{tan4}{x}\right) \\ $$$${f}\left({x}\right)\:=\:\frac{\left(\mathrm{cos}{x}+\mathrm{sin}{x}\right)\left(\mathrm{cos4}{x}+\mathrm{sin4}{x}\right)}{\mathrm{cos}{x}\mathrm{cos4}{x}} \\ $$$${f}\left({x}\right)\:=\:\frac{\mathrm{cos}{x}\mathrm{cos4}{x}+\mathrm{sin}{x}\mathrm{sin4}{x}+\mathrm{sin}{x}\mathrm{cos4}{x}+\mathrm{cos}{x}\mathrm{sin4}{x}}{\mathrm{cos}{x}\mathrm{cos4}{x}} \\ $$$${f}\left({x}\right)\:=\:\frac{\mathrm{cos3}{x}+\mathrm{sin5}{x}}{\mathrm{cos}{x}\mathrm{cos4}{x}} \\ $$$${f}\left({x}\right)\:=\:\frac{\mathrm{cos3}{x}+\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}−\mathrm{5}{x}\right)}{\mathrm{cos}{x}\mathrm{cos4}{x}} \\ $$$${f}\left({x}\right)\:=\:\frac{\mathrm{2cos}\left(\frac{\mathrm{3}{x}+\frac{\pi}{\mathrm{2}}−\mathrm{5}{x}}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\mathrm{3}{x}−\frac{\pi}{\mathrm{2}}+\mathrm{5}{x}}{\mathrm{2}}\right)}{\mathrm{cos}{x}\mathrm{cos4}{x}} \\ $$$${f}\left({x}\right)\:=\:\frac{\mathrm{2cos}\left({x}−\frac{\pi}{\mathrm{4}}\right)\mathrm{cos}\left(\mathrm{4}{x}−\frac{\pi}{\mathrm{4}}\right)}{\mathrm{cos}{x}\mathrm{cos4}{x}} \\ $$$${f}\left({x}\right)\:=\:\mathrm{2}\:\Leftrightarrow\:\mathrm{cos}\left({x}−\frac{\pi}{\mathrm{4}}\right)\mathrm{cos}\left(\mathrm{4}{x}−\frac{\pi}{\mathrm{4}}\right)\:=\:\mathrm{cos}{x}\mathrm{cos4}{x} \\ $$$$\Leftrightarrow\:\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{cos3}{x}+\mathrm{cos}\left(\mathrm{5}{x}−\frac{\pi}{\mathrm{2}}\right)\right]\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{cos3}{x}+\mathrm{cos5}{x}\right] \\ $$$$\Leftrightarrow\:\mathrm{cos}\left(\mathrm{5}{x}−\frac{\pi}{\mathrm{2}}\right)\:=\:\mathrm{cos5}{x} \\ $$$$\Leftrightarrow\:\mathrm{5}{x}−\frac{\pi}{\mathrm{2}}\:=\:\pm\mathrm{5}{x}+\mathrm{2}{k}\pi,\:{k}\in\mathbb{Z} \\ $$$$\Leftrightarrow\:{x}\:=\:\frac{\pi}{\mathrm{20}}\:+\frac{{k}\pi}{\mathrm{10}},\:{k}\in\mathbb{Z} \\ $$$$\mathcal{S}\:=\:\left\{\frac{\pi}{\mathrm{20}}+\frac{{k}\pi}{\mathrm{10}},\:{k}\in\mathbb{Z}\right\} \\ $$$$\mathrm{Numerically}\:\mathrm{we}\:\mathrm{can}\:\mathrm{verify}\:\mathrm{for}\:\mathrm{example} \\ $$$$\mathrm{that},\:\mathrm{for}\:{k}\:=\:\mathrm{0}\:: \\ $$$$\left(\mathrm{1}+\mathrm{tan}\frac{\pi}{\mathrm{20}}\right)\left(\mathrm{1}+\mathrm{tan}\frac{\pi}{\mathrm{5}}\right)\:=\:\mathrm{2} \\ $$
Commented by liberty last updated on 10/Jan/21

$$\mathrm{correct}\:\mathrm{sir} \\ $$
