Question Number 43540 by abdo.msup.com last updated on 11/Sep/18

$${prove}\:{that}\:\mathrm{111}\:{divide}\:\mathrm{10}^{\mathrm{6}{n}+\mathrm{2}} \:+\mathrm{10}^{\mathrm{3}{n}+\mathrm{1}} \:+\mathrm{1} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 12/Sep/18
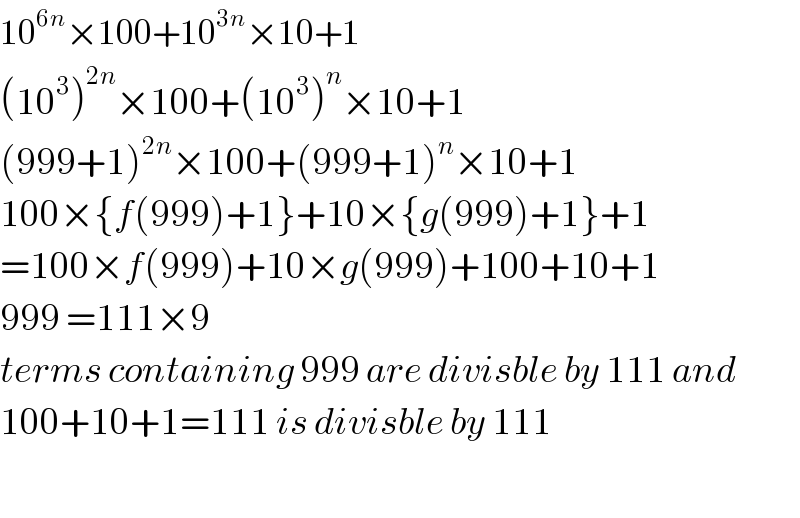
$$\mathrm{10}^{\mathrm{6}{n}} ×\mathrm{100}+\mathrm{10}^{\mathrm{3}{n}} ×\mathrm{10}+\mathrm{1} \\ $$$$\left(\mathrm{10}^{\mathrm{3}} \right)^{\mathrm{2}{n}} ×\mathrm{100}+\left(\mathrm{10}^{\mathrm{3}} \right)^{{n}} ×\mathrm{10}+\mathrm{1} \\ $$$$\left(\mathrm{999}+\mathrm{1}\right)^{\mathrm{2}{n}} ×\mathrm{100}+\left(\mathrm{999}+\mathrm{1}\right)^{{n}} ×\mathrm{10}+\mathrm{1} \\ $$$$\mathrm{100}×\left\{{f}\left(\mathrm{999}\right)+\mathrm{1}\right\}+\mathrm{10}×\left\{{g}\left(\mathrm{999}\right)+\mathrm{1}\right\}+\mathrm{1} \\ $$$$=\mathrm{100}×{f}\left(\mathrm{999}\right)+\mathrm{10}×{g}\left(\mathrm{999}\right)+\mathrm{100}+\mathrm{10}+\mathrm{1} \\ $$$$\mathrm{999}\:=\mathrm{111}×\mathrm{9} \\ $$$${terms}\:{containing}\:\mathrm{999}\:{are}\:{divisble}\:{by}\:\mathrm{111}\:{and} \\ $$$$\mathrm{100}+\mathrm{10}+\mathrm{1}=\mathrm{111}\:{is}\:{divisble}\:{by}\:\mathrm{111} \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 12/Sep/18
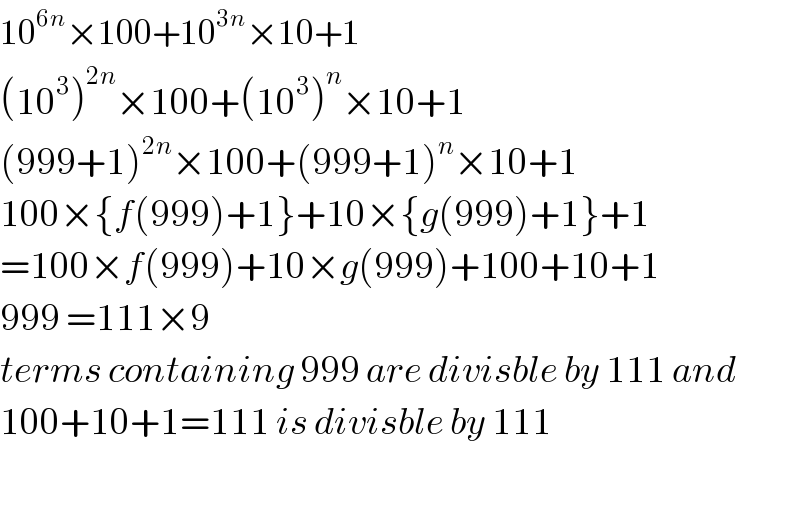
$$\mathrm{10}^{\mathrm{6}{n}} ×\mathrm{100}+\mathrm{10}^{\mathrm{3}{n}} ×\mathrm{10}+\mathrm{1} \\ $$$$\left(\mathrm{10}^{\mathrm{3}} \right)^{\mathrm{2}{n}} ×\mathrm{100}+\left(\mathrm{10}^{\mathrm{3}} \right)^{{n}} ×\mathrm{10}+\mathrm{1} \\ $$$$\left(\mathrm{999}+\mathrm{1}\right)^{\mathrm{2}{n}} ×\mathrm{100}+\left(\mathrm{999}+\mathrm{1}\right)^{{n}} ×\mathrm{10}+\mathrm{1} \\ $$$$\mathrm{100}×\left\{{f}\left(\mathrm{999}\right)+\mathrm{1}\right\}+\mathrm{10}×\left\{{g}\left(\mathrm{999}\right)+\mathrm{1}\right\}+\mathrm{1} \\ $$$$=\mathrm{100}×{f}\left(\mathrm{999}\right)+\mathrm{10}×{g}\left(\mathrm{999}\right)+\mathrm{100}+\mathrm{10}+\mathrm{1} \\ $$$$\mathrm{999}\:=\mathrm{111}×\mathrm{9} \\ $$$${terms}\:{containing}\:\mathrm{999}\:{are}\:{divisble}\:{by}\:\mathrm{111}\:{and} \\ $$$$\mathrm{100}+\mathrm{10}+\mathrm{1}=\mathrm{111}\:{is}\:{divisble}\:{by}\:\mathrm{111} \\ $$$$ \\ $$
