Question Number 173888 by azadsir last updated on 20/Jul/22

$$\mathrm{Prove}\:\mathrm{that},\:\frac{\mathrm{13x}}{\mathrm{x}^{\mathrm{2}} −\sqrt{\mathrm{13x}}+\mathrm{1}}\:=\:\sqrt{\mathrm{13}}\:\mathrm{if},\:\mathrm{x}\:=\:\sqrt{\mathrm{13}}\:+\:\mathrm{2}\sqrt{\mathrm{3}}\: \\ $$
Answered by a.lgnaoui last updated on 20/Jul/22
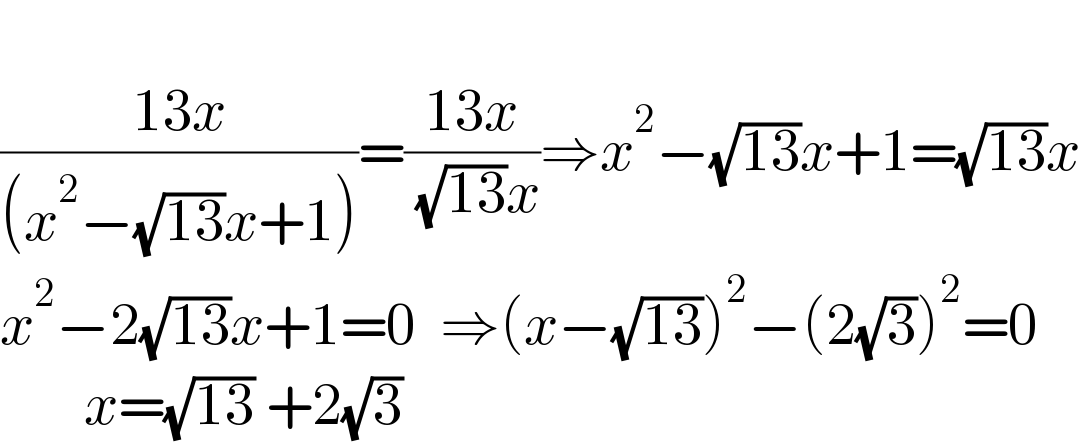
$$ \\ $$$$\frac{\mathrm{13}{x}}{\left({x}^{\mathrm{2}} −\sqrt{\mathrm{13}}{x}+\mathrm{1}\right)}=\frac{\mathrm{13}{x}}{\:\sqrt{\mathrm{13}}{x}}\Rightarrow{x}^{\mathrm{2}} −\sqrt{\mathrm{13}}{x}+\mathrm{1}=\sqrt{\mathrm{13}}{x} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{13}}{x}+\mathrm{1}=\mathrm{0}\:\:\Rightarrow\left({x}−\sqrt{\mathrm{13}}\right)^{\mathrm{2}} −\left(\mathrm{2}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:{x}=\sqrt{\mathrm{13}}\:+\mathrm{2}\sqrt{\mathrm{3}} \\ $$
