Question Number 43543 by peter frank last updated on 11/Sep/18
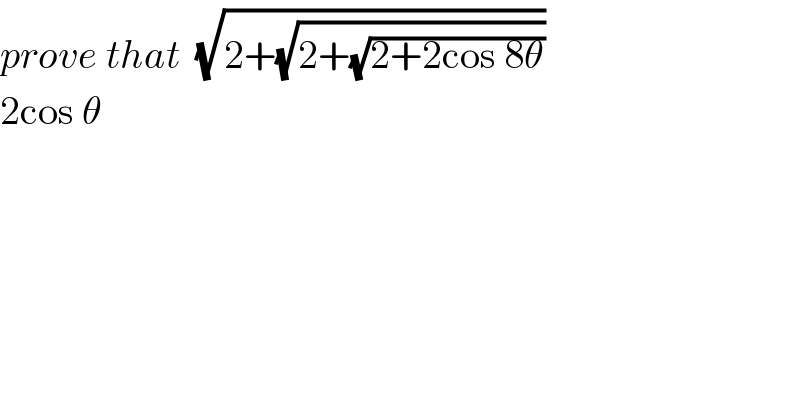
$${prove}\:{that}\:\:\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\mathrm{2cos}\:\mathrm{8}\theta}}} \\ $$$$\mathrm{2cos}\:\theta \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 12/Sep/18
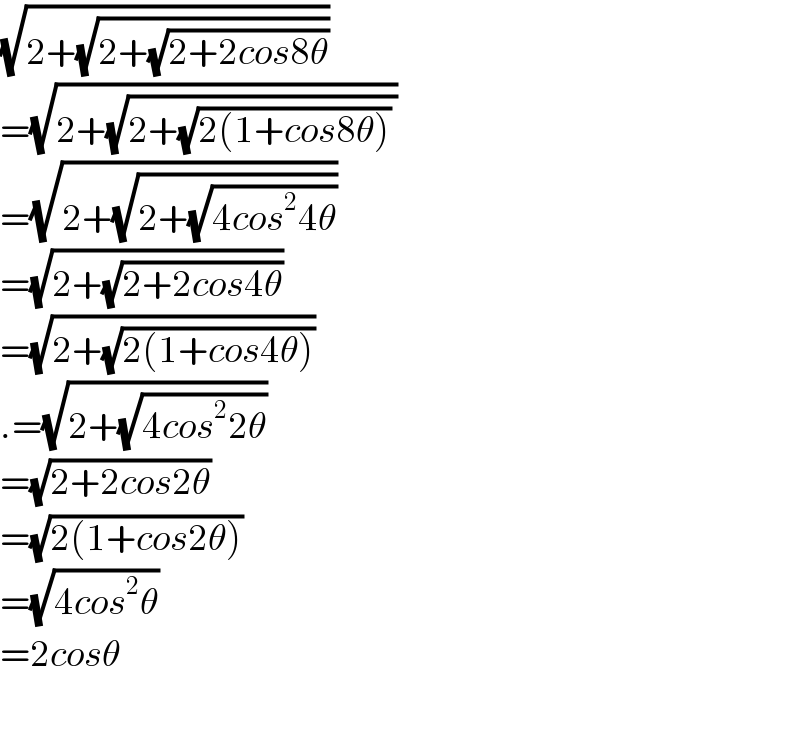
$$\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\mathrm{2}{cos}\mathrm{8}\theta}}} \\ $$$$=\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}\left(\mathrm{1}+{cos}\mathrm{8}\theta\right)}\:}} \\ $$$$=\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{4}{cos}^{\mathrm{2}} \mathrm{4}\theta}}} \\ $$$$=\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\mathrm{2}{cos}\mathrm{4}\theta}} \\ $$$$=\sqrt{\mathrm{2}+\sqrt{\mathrm{2}\left(\mathrm{1}+{cos}\mathrm{4}\theta\right)}} \\ $$$$.=\sqrt{\mathrm{2}+\sqrt{\mathrm{4}{cos}^{\mathrm{2}} \mathrm{2}\theta}} \\ $$$$=\sqrt{\mathrm{2}+\mathrm{2}{cos}\mathrm{2}\theta} \\ $$$$=\sqrt{\mathrm{2}\left(\mathrm{1}+{cos}\mathrm{2}\theta\right)} \\ $$$$=\sqrt{\mathrm{4}{cos}^{\mathrm{2}} \theta} \\ $$$$=\mathrm{2}{cos}\theta \\ $$$$ \\ $$
