Question Number 161745 by HongKing last updated on 21/Dec/21
![Prove that: 3 (√e) = (1/3) Σ_(k=1) ^∞ [ Σ_(n=0) ^∞ (1/(n!)) ]k2^(-k)](https://www.tinkutara.com/question/Q161745.png)
$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\mathrm{3}\:\sqrt{\mathrm{e}}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\infty} {\sum}}\:\left[\:\underset{\boldsymbol{\mathrm{n}}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{n}!}\:\right]\mathrm{k2}^{-\boldsymbol{\mathrm{k}}} \\ $$
Commented by mr W last updated on 22/Dec/21
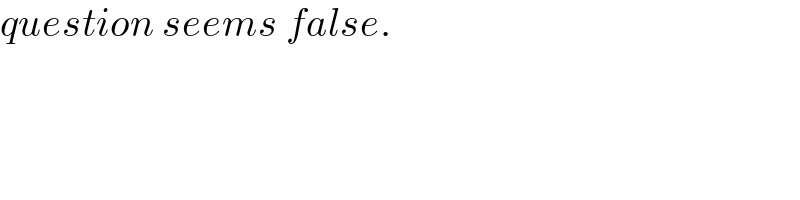
$${question}\:{seems}\:{false}. \\ $$
Answered by mr W last updated on 22/Dec/21
![Σ_(k=1) ^∞ x^k =(x/(1−x)) for ∣x∣<1 Σ_(k=1) ^∞ kx^(k−1) =(1/(1−x))+(x/((1−x)^2 )) Σ_(k=1) ^∞ kx^k =(x/(1−x))+(x^2 /((1−x)^2 )) with x=(1/2) ⇒Σ_(k=1) ^∞ k2^(−k) =((1/2)/(1−(1/2)))+((((1/2))^2 )/((1−(1/2))^2 ))=2 e^x =Σ_(n=0) ^∞ (x^n /(n!)) with x=1 ⇒Σ_(n=0) ^∞ (1/(n!))=e (1/3) Σ_(k=1) ^∞ [ Σ_(n=0) ^∞ (1/(n!)) ]k2^(-k) =(1/3) Σ_(k=1) ^∞ (e) k2^(-k) =(e/3) Σ_(k=1) ^∞ k2^(-k) =(e/3)×2 =((2e)/3)≠3(√e)](https://www.tinkutara.com/question/Q161756.png)
$$\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}{x}^{{k}} =\frac{{x}}{\mathrm{1}−{x}}\:{for}\:\mid{x}\mid<\mathrm{1} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}{kx}^{{k}−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{1}−{x}}+\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} } \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}{kx}^{{k}} =\frac{{x}}{\mathrm{1}−{x}}+\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} } \\ $$$${with}\:{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}{k}\mathrm{2}^{−{k}} =\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}+\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }=\mathrm{2} \\ $$$${e}^{{x}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}!} \\ $$$${with}\:{x}=\mathrm{1} \\ $$$$\Rightarrow\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}={e} \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\:\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\infty} {\sum}}\:\left[\:\underset{\boldsymbol{\mathrm{n}}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{n}!}\:\right]\mathrm{k2}^{-\boldsymbol{\mathrm{k}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\:\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\infty} {\sum}}\:\left({e}\right)\:\mathrm{k2}^{-\boldsymbol{\mathrm{k}}} \\ $$$$=\frac{{e}}{\mathrm{3}}\:\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{k2}^{-\boldsymbol{\mathrm{k}}} \\ $$$$=\frac{{e}}{\mathrm{3}}×\mathrm{2} \\ $$$$=\frac{\mathrm{2}{e}}{\mathrm{3}}\neq\mathrm{3}\sqrt{{e}} \\ $$
Commented by HongKing last updated on 22/Dec/21
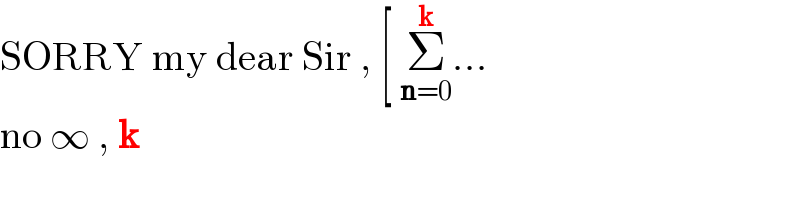
$$\mathrm{SORRY}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir}\:,\:\left[\:\underset{\boldsymbol{\mathrm{n}}=\mathrm{0}} {\overset{\boldsymbol{\mathrm{k}}} {\sum}}…\right. \\ $$$$\mathrm{no}\:\infty\:,\:\boldsymbol{\mathrm{k}} \\ $$
