Menu Close

Prove-that-3-m-3-n-1-is-not-a-perfect-square-where-m-and-n-are-positive-integers-

Tinku Tara 0 Comments
Pin




Question Number 34429 by $@ty@m last updated on 06/May/18
Prove that 3^m +3^n +1 is not a perfect square. where m and n are positive integers.
$${Prove}\:{that} \\ $$$$\mathrm{3}^{{m}} +\mathrm{3}^{{n}} +\mathrm{1}\:{is}\:{not}\:{a}\:{perfect}\:{square}. \\ $$$${where}\:{m}\:{and}\:{n}\:{are}\:{positive}\:{integers}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 06/May/18
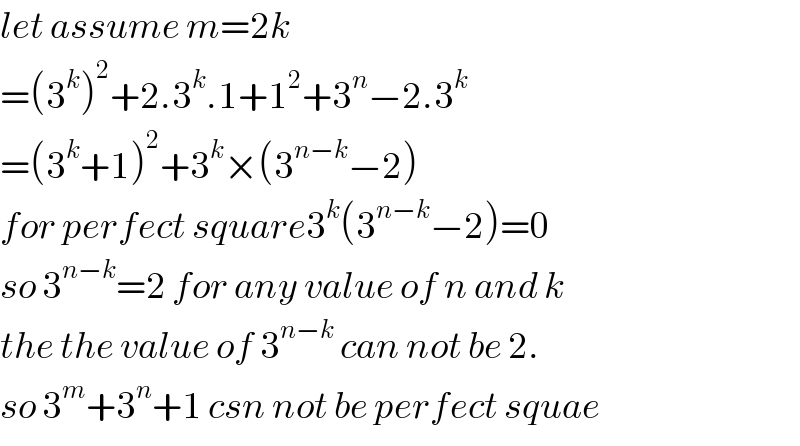
let assume m=2k =(3^k )^2 +2.3^k .1+1^2 +3^n −2.3^k =(3^k +1)^2 +3^k ×(3^(n−k) −2) for perfect square3^k (3^(n−k) −2)=0 so 3^(n−k) =2 for any value of n and k the the value of 3^(n−k) can not be 2. so 3^m +3^n +1 csn not be perfect squae
$${let}\:{assume}\:{m}=\mathrm{2}{k} \\ $$$$=\left(\mathrm{3}^{{k}} \right)^{\mathrm{2}} +\mathrm{2}.\mathrm{3}^{{k}} .\mathrm{1}+\mathrm{1}^{\mathrm{2}} +\mathrm{3}^{{n}} −\mathrm{2}.\mathrm{3}^{{k}} \\ $$$$=\left(\mathrm{3}^{{k}} +\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}^{{k}} ×\left(\mathrm{3}^{{n}−{k}} −\mathrm{2}\right) \\ $$$${for}\:{perfect}\:{square}\mathrm{3}^{{k}} \left(\mathrm{3}^{{n}−{k}} −\mathrm{2}\right)=\mathrm{0} \\ $$$${so}\:\mathrm{3}^{{n}−{k}} =\mathrm{2}\:{for}\:{any}\:{value}\:{of}\:{n}\:{and}\:{k} \\ $$$${the}\:{the}\:{value}\:{of}\:\mathrm{3}^{{n}−{k}} \:{can}\:{not}\:{be}\:\mathrm{2}. \\ $$$${so}\:\mathrm{3}^{{m}} +\mathrm{3}^{{n}} +\mathrm{1}\:{csn}\:{not}\:{be}\:{perfect}\:{squae} \\ $$
Commented by $@ty@m last updated on 06/May/18
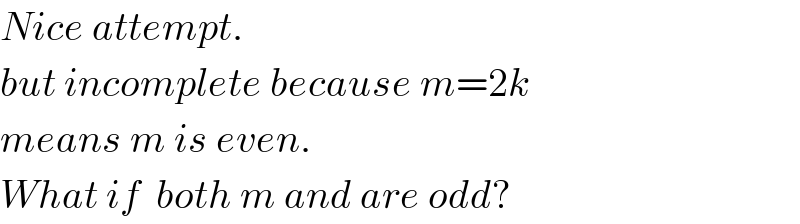
Nice attempt. but incomplete because m=2k means m is even. What if both m and are odd?
$${Nice}\:{attempt}. \\ $$$${but}\:{incomplete}\:{because}\:{m}=\mathrm{2}{k} \\ $$$${means}\:{m}\:{is}\:{even}. \\ $$$${What}\:{if}\:\:{both}\:{m}\:{and}\:{are}\:{odd}? \\ $$
Commented by Rasheed.Sindhi last updated on 07/May/18
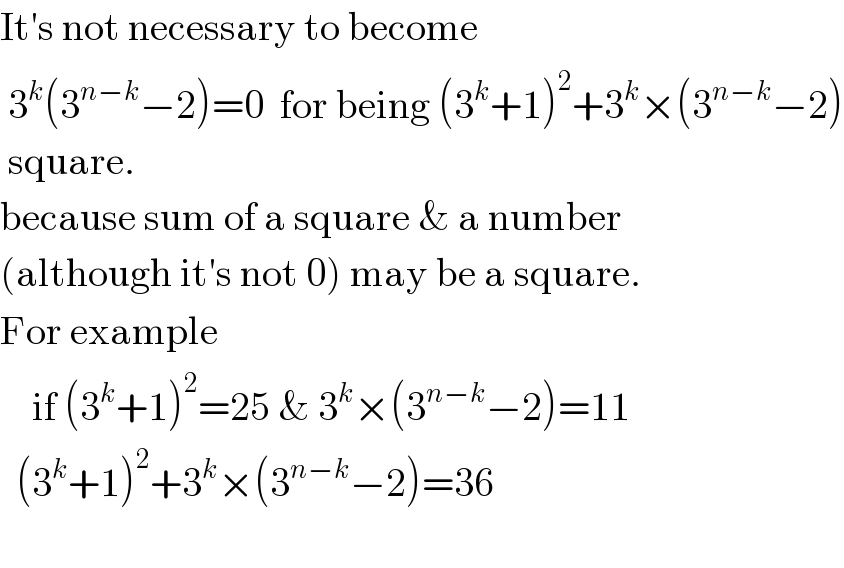
It′s not necessary to become 3^k (3^(n−k) −2)=0 for being (3^k +1)^2 +3^k ×(3^(n−k) −2) square. because sum of a square & a number (although it′s not 0) may be a square. For example if (3^k +1)^2 =25 & 3^k ×(3^(n−k) −2)=11 (3^k +1)^2 +3^k ×(3^(n−k) −2)=36
$$\mathrm{It}'\mathrm{s}\:\mathrm{not}\:\mathrm{necessary}\:\mathrm{to}\:\mathrm{become} \\ $$$$\:\mathrm{3}^{{k}} \left(\mathrm{3}^{{n}−{k}} −\mathrm{2}\right)=\mathrm{0}\:\:\mathrm{for}\:\mathrm{being}\:\left(\mathrm{3}^{{k}} +\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}^{{k}} ×\left(\mathrm{3}^{{n}−{k}} −\mathrm{2}\right) \\ $$$$\:\mathrm{square}. \\ $$$$\mathrm{because}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{a}\:\mathrm{square}\:\&\:\mathrm{a}\:\mathrm{number} \\ $$$$\left(\mathrm{although}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{0}\right)\:\mathrm{may}\:\mathrm{be}\:\mathrm{a}\:\mathrm{square}.\: \\ $$$$\mathrm{For}\:\mathrm{example}\: \\ $$$$\:\:\:\:\mathrm{if}\:\left(\mathrm{3}^{{k}} +\mathrm{1}\right)^{\mathrm{2}} =\mathrm{25}\:\&\:\mathrm{3}^{{k}} ×\left(\mathrm{3}^{{n}−{k}} −\mathrm{2}\right)=\mathrm{11} \\ $$$$\:\:\left(\mathrm{3}^{{k}} +\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}^{{k}} ×\left(\mathrm{3}^{{n}−{k}} −\mathrm{2}\right)=\mathrm{36} \\ $$$$\:\:\:\:\:\: \\ $$
Answered by Rasheed.Sindhi last updated on 08/May/18
3^m ,3^n & 1 are odd numbers. ∵ The sum of three odd numbers is odd ∴ 3^m +3^n +1 is an odd number. And if it were perfect square,it must have been square of an odd number.[Square of an even number is even of course.] Let 3^m +3^n +1=(2k+1)^2 3^m +3^n +1=4k^2 +4k+1 3^m +3^n =4k^2 +4k 3^m +3^n =4(k^2 +k) k^2 +k∈E, so right side is divisible by 8 whereas left side is not divisible by 8 (See proof at the end)^∗ ∵ 3^m +3^n +1 cannot be square of even nunmber. because it an odd number. ∵ 3^m +3^n +1 cannot be square of odd nunmber due to the above contrdiction. ∴ 3^m +3^n +1 can′t be perfect square. −−−−−−−−−−− ∗ 3^m (mod 8)=1 or 3 3^m +3^n (mod 8)=2,4,6 only ∴ 3^m +3^n (mod 8)≠0 I-e 3^m +3^n is not divisible by 8
$$\mathrm{3}^{\mathrm{m}} ,\mathrm{3}^{\mathrm{n}} \&\:\mathrm{1}\:\mathrm{are}\:\mathrm{odd}\:\mathrm{numbers}. \\ $$$$\:\because\:\mathrm{The}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{three}\:\mathrm{odd}\:\mathrm{numbers}\:\mathrm{is}\:\mathrm{odd} \\ $$$$\:\therefore\:\:\mathrm{3}^{\mathrm{m}} +\mathrm{3}^{\mathrm{n}} +\mathrm{1}\:\mathrm{is}\:\mathrm{an}\:\mathrm{odd}\:\mathrm{number}. \\ $$$$\mathrm{And}\:\mathrm{if}\:\mathrm{it}\:\boldsymbol{\mathrm{were}}\:\mathrm{perfect}\:\mathrm{square},\mathrm{it}\:\mathrm{must}\:\mathrm{have}\:\mathrm{been} \\ $$$$\mathrm{square}\:\mathrm{of}\:\mathrm{an}\:\mathrm{odd}\:\mathrm{number}.\left[\mathrm{Square}\:\mathrm{of}\:\mathrm{an}\right. \\ $$$$\left.\mathrm{even}\:\mathrm{number}\:\mathrm{is}\:\mathrm{even}\:\mathrm{of}\:\mathrm{course}.\right] \\ $$$$\mathrm{Let}\:\mathrm{3}^{\mathrm{m}} +\mathrm{3}^{\mathrm{n}} +\mathrm{1}=\left(\mathrm{2k}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{3}^{\mathrm{m}} +\mathrm{3}^{\mathrm{n}} +\mathrm{1}=\mathrm{4k}^{\mathrm{2}} +\mathrm{4k}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{3}^{\mathrm{m}} +\mathrm{3}^{\mathrm{n}} =\mathrm{4k}^{\mathrm{2}} +\mathrm{4k} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{3}^{\mathrm{m}} +\mathrm{3}^{\mathrm{n}} =\mathrm{4}\left(\mathrm{k}^{\mathrm{2}} +\mathrm{k}\right) \\ $$$$\mathrm{k}^{\mathrm{2}} +\mathrm{k}\in\mathbb{E},\:\mathrm{so}\:\mathrm{right}\:\mathrm{side}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{divisible}}\:\mathrm{by}\:\mathrm{8} \\ $$$$\mathrm{whereas}\:\mathrm{left}\:\mathrm{side}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{not}}\:\boldsymbol{\mathrm{divisible}}\:\mathrm{by}\:\mathrm{8} \\ $$$$\left(\mathrm{See}\:\mathrm{proof}\:\mathrm{at}\:\mathrm{the}\:\mathrm{end}\right)^{\ast} \\ $$$$\:\because\:\mathrm{3}^{\mathrm{m}} +\mathrm{3}^{\mathrm{n}} +\mathrm{1}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{square}\:\mathrm{of}\:\mathrm{even}\:\mathrm{nunmber}. \\ $$$$\mathrm{because}\:\mathrm{it}\:\mathrm{an}\:\mathrm{odd}\:\mathrm{number}. \\ $$$$\:\because\:\mathrm{3}^{\mathrm{m}} +\mathrm{3}^{\mathrm{n}} +\mathrm{1}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{square}\:\mathrm{of}\:\mathrm{odd}\:\mathrm{nunmber} \\ $$$$\mathrm{due}\:\mathrm{to}\:\mathrm{the}\:\mathrm{above}\:\mathrm{contrdiction}. \\ $$$$\:\therefore\:\mathrm{3}^{\mathrm{m}} +\mathrm{3}^{\mathrm{n}} +\mathrm{1}\:\mathrm{can}'\mathrm{t}\:\mathrm{be}\:\mathrm{perfect}\:\mathrm{square}. \\ $$$$\:\:\:\:\:\:\:\:\:\:−−−−−−−−−−− \\ $$$$\ast\:\mathrm{3}^{\mathrm{m}} \left(\mathrm{mod}\:\mathrm{8}\right)=\mathrm{1}\:\mathrm{or}\:\mathrm{3} \\ $$$$\:\:\:\:\:\mathrm{3}^{\mathrm{m}} +\mathrm{3}^{\mathrm{n}} \left(\mathrm{mod}\:\mathrm{8}\right)=\mathrm{2},\mathrm{4},\mathrm{6}\:\mathrm{only} \\ $$$$\therefore\:\:\mathrm{3}^{\mathrm{m}} +\mathrm{3}^{\mathrm{n}} \left(\mathrm{mod}\:\mathrm{8}\right)\neq\mathrm{0} \\ $$$$\:\:\:\:\:\:\mathrm{I}-\mathrm{e}\:\mathrm{3}^{\mathrm{m}} +\mathrm{3}^{\mathrm{n}} \:\mathrm{is}\:\mathrm{not}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{8} \\ $$
Commented by MJS last updated on 09/May/18
great!
$$\mathrm{great}! \\ $$
Commented by MrW3 last updated on 14/Jun/18
wonderful proof!
$${wonderful}\:{proof}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *