prove-that-3-n-1-is-a-multiple-of-2-by-mathematical-induction-

Question Number 24822 by NECx last updated on 26/Nov/17

p r o v e t h a t 3^{n} - 1 i s a m u l t i p l e o f 2

b y m a t h e m a t i c a l i n d u c t i o n

Commented by maxmathsup by imad last updated on 24/May/19

n = 0 \to 3^{0} - 1 = 0 m u l t i p l e o f 2 l e t s u p p o s e 3^{n} - 1 m u l t i p l e o f 2 \Rightarrow

3^{n} - 1 = 2 k \Rightarrow 3^{n + 1} - 1 = 3^{n} . 3 = (2 k + 1) 3 - 1 = 6 k + 3 - 1 = 6 k + 2

2 (3 k + 1) = 2 k^{^{'}} w i t h k^{^{'}} = 3 k + 1 s o t h e r e l a t i o n i s t r u e a t t e r m n + 1 .

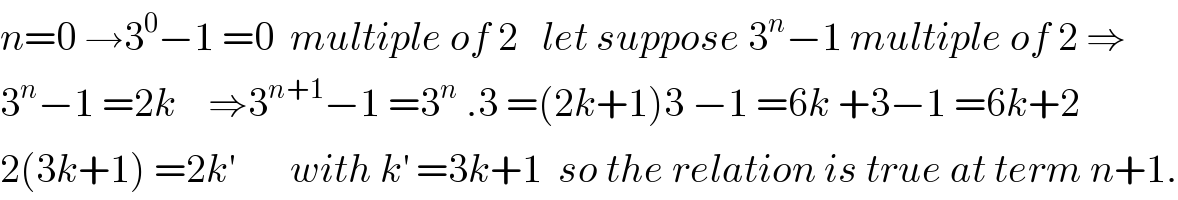
Answered by jota+ last updated on 27/Nov/17

3^{1} - 1 = \dot{2}

3^{k} - 1 = \dot{2} h i p o t e s i s

3 (3^{k} - 1) = 3 \times \dot{2}

3^{k + 1} - 3 = \dot{2}

3^{k + 1} - 1 = \dot{2} + 2 = \dot{2}

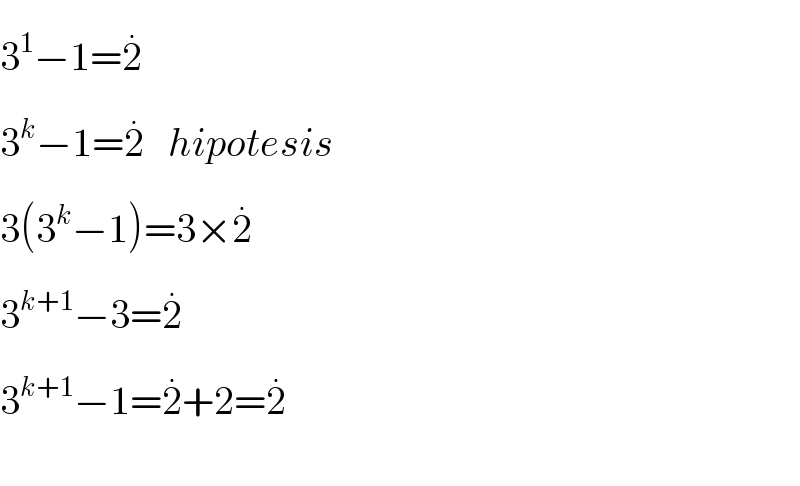
Commented by Rasheed.Sindhi last updated on 27/Nov/17

Also like your notation (\dot{2})

for^{'} multiple of 2^{'}

Commented by math solver last updated on 27/Nov/17

i guess this is usual notation in spain .

Commented by Rasheed.Sindhi last updated on 27/Nov/17

But I see it for first time!

Reason may be that I {haven}^{'} t

read so many math books .