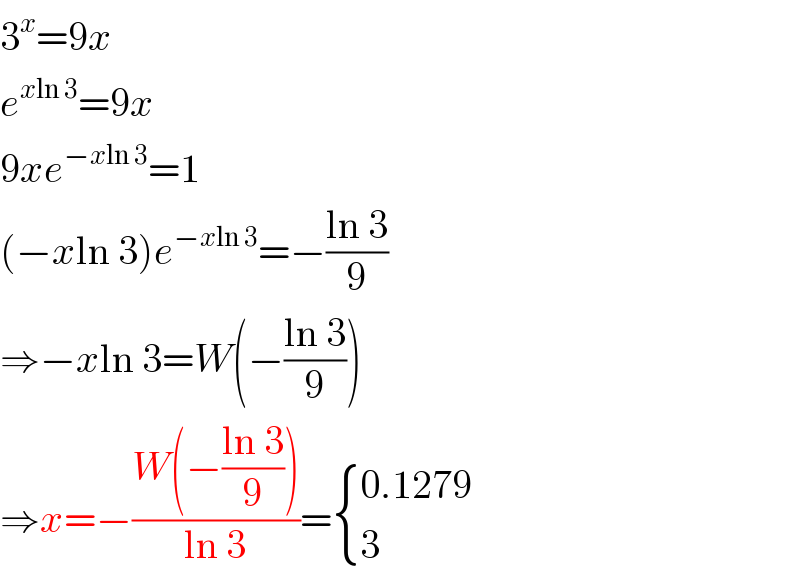prove-that-3-x-9x-

Question Number 35491 by mondodotto@gmail.com last updated on 19/May/18

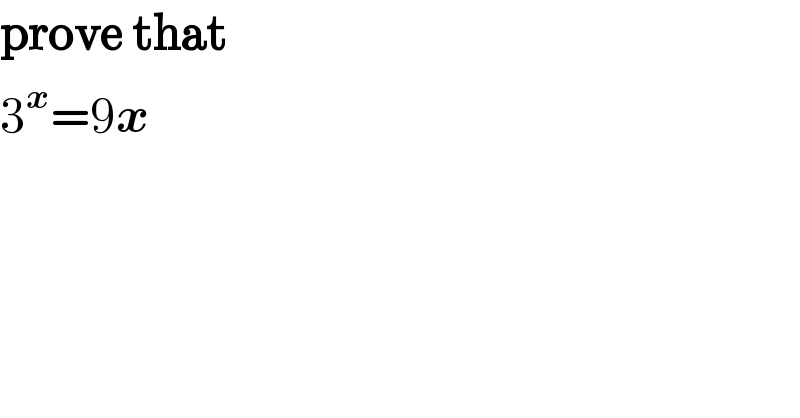
prove that

3^{x} = 9 x

Commented by math khazana by abdo last updated on 12/Jun/18

t h e q u e s t i o n i s n o t c o r r e c t i t s o n l y a e q u a t i o n

b e c a u s e y = 9 x i s e q u a t i o n o f a l i n e y = 3^{x} = e^{x l n (3)}

n e v e r b e a e q u a t i o n o f a l i n e!

Answered by candre last updated on 19/May/18

x = 0 \Rightarrow 3^{x} = 1 \neq 0 = 9 x

therefore afirmation is false

Commented by Rasheed.Sindhi last updated on 19/May/18

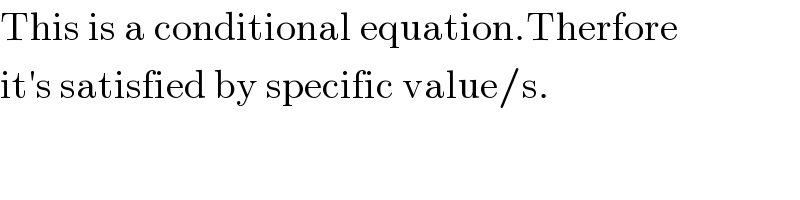
This is a conditional equation . Therfore

{it}^{'} s satisfied by specific value / s .

Commented by candre last updated on 20/May/18

but if it was that would it be

“ find x such afirmation is {true}^{″} ?

Commented by Rasheed.Sindhi last updated on 20/May/18

Sir you are right, the questioner

has written “ Prove {that}^{″} . I {didn}^{'} t

consider it at first .

Answered by rahul 19 last updated on 20/May/18

3^{3} = 9 \times 3

\Rightarrow x = 3 .

Answered by MrW3 last updated on 12/Jun/18

3^{x} = 9 x

e^{x \ln 3} = 9 x

9 {x e}^{- x \ln 3} = 1

(- x \ln 3) e^{- x \ln 3} = - \frac{\ln 3}{9}

\Rightarrow - x \ln 3 = W (- \frac{\ln 3}{9})

\Rightarrow x = - \frac{W (- \frac{\ln 3}{9})}{\ln 3} = {\begin{cases} 0.1279 \\ 3 \end{cases}

Facebook Tweet Pin