Question Number 15967 by tawa tawa last updated on 16/Jun/17
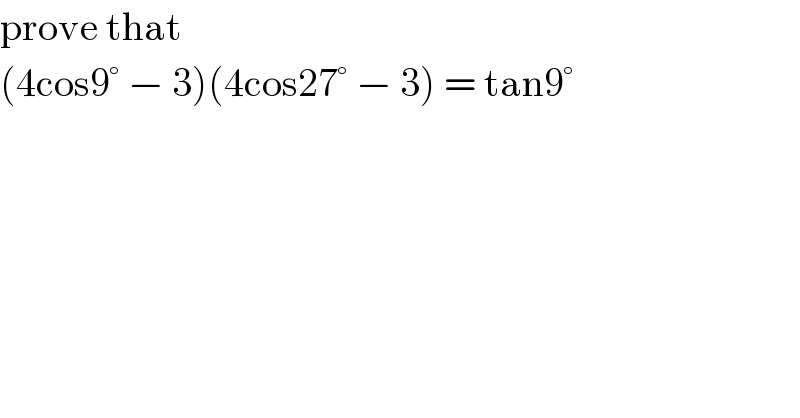
$$\mathrm{prove}\:\mathrm{that} \\ $$$$\left(\mathrm{4cos9}°\:−\:\mathrm{3}\right)\left(\mathrm{4cos27}°\:−\:\mathrm{3}\right)\:=\:\mathrm{tan9}° \\ $$
Commented by sandy_suhendra last updated on 16/Jun/17
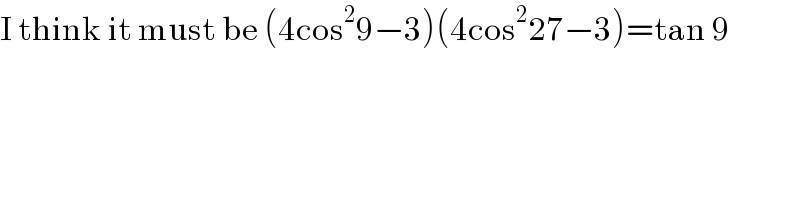
$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{must}\:\mathrm{be}\:\left(\mathrm{4cos}^{\mathrm{2}} \mathrm{9}−\mathrm{3}\right)\left(\mathrm{4cos}^{\mathrm{2}} \mathrm{27}−\mathrm{3}\right)=\mathrm{tan}\:\mathrm{9} \\ $$
Answered by sandy_suhendra last updated on 16/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 16/Jun/17
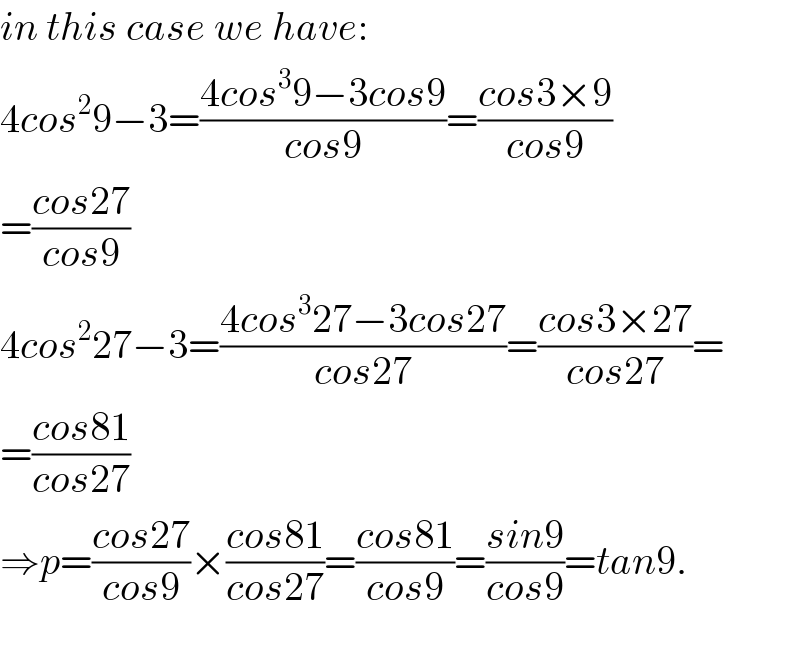
$${in}\:{this}\:{case}\:{we}\:{have}: \\ $$$$\mathrm{4}{cos}^{\mathrm{2}} \mathrm{9}−\mathrm{3}=\frac{\mathrm{4}{cos}^{\mathrm{3}} \mathrm{9}−\mathrm{3}{cos}\mathrm{9}}{{cos}\mathrm{9}}=\frac{{cos}\mathrm{3}×\mathrm{9}}{{cos}\mathrm{9}} \\ $$$$=\frac{{cos}\mathrm{27}}{{cos}\mathrm{9}} \\ $$$$\mathrm{4}{cos}^{\mathrm{2}} \mathrm{27}−\mathrm{3}=\frac{\mathrm{4}{cos}^{\mathrm{3}} \mathrm{27}−\mathrm{3}{cos}\mathrm{27}}{{cos}\mathrm{27}}=\frac{{cos}\mathrm{3}×\mathrm{27}}{{cos}\mathrm{27}}= \\ $$$$=\frac{{cos}\mathrm{81}}{{cos}\mathrm{27}} \\ $$$$\Rightarrow{p}=\frac{{cos}\mathrm{27}}{{cos}\mathrm{9}}×\frac{{cos}\mathrm{81}}{{cos}\mathrm{27}}=\frac{{cos}\mathrm{81}}{{cos}\mathrm{9}}=\frac{{sin}\mathrm{9}}{{cos}\mathrm{9}}={tan}\mathrm{9}. \\ $$$$ \\ $$
Commented by tawa tawa last updated on 16/Jun/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$
