Prove-that-6n-is-divisible-by-2-2n-3-n-

Question Number 21404 by Tinkutara last updated on 23/Sep/17

Prove that (6 n)! is divisible by 2^{2 n} . 3^{n} .

Answered by dioph last updated on 23/Sep/17

if n > 1, there are at least 3 n even

numbers and 2 n multiples of 3 in

[1, 6 n], so that (6 n)! is divisible by

2^{3 n} . 3^{2 n} and, in particular, by 2^{2 n} . 3^{n}

Commented by Tinkutara last updated on 23/Sep/17

Can you explain 1^{st} and 2^{nd} lines ?

Commented by dioph last updated on 23/Sep/17

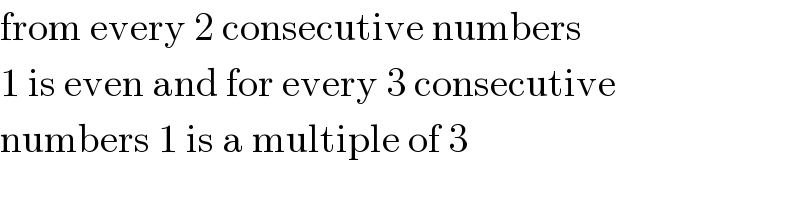
from every 2 consecutive numbers

1 is even and for every 3 consecutive

numbers 1 is a multiple of 3

Commented by Tinkutara last updated on 23/Sep/17

Thank you very much Sir!