Question Number 116941 by Her_Majesty last updated on 08/Oct/20
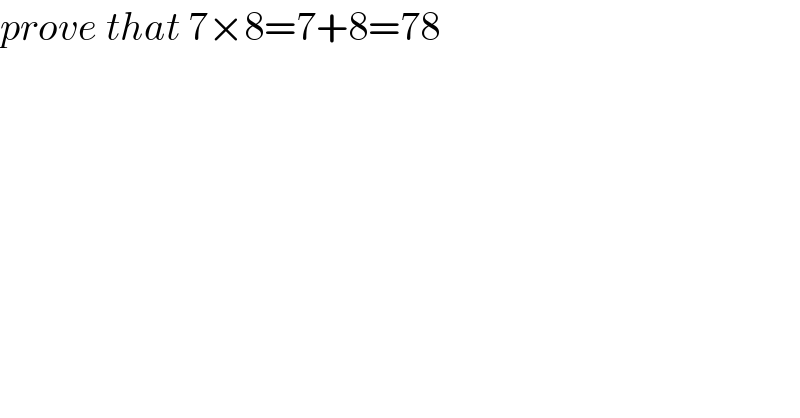
$${prove}\:{that}\:\mathrm{7}×\mathrm{8}=\mathrm{7}+\mathrm{8}=\mathrm{78} \\ $$
Commented by MJS_new last updated on 08/Oct/20

$$\mathrm{one}\:\mathrm{possible}\:“\mathrm{proof}'' \\ $$$$\begin{cases}{\mathrm{1}=\mathrm{e}^{\mathrm{2}\pi\mathrm{i}} }\\{\mathrm{1}=\mathrm{e}^{\mathrm{4}\pi\mathrm{i}} }\end{cases}\:\Leftrightarrow\:\mathrm{2}\pi\mathrm{i}=\mathrm{4}\pi\mathrm{i}\:\Leftrightarrow\:\mathrm{2}=\mathrm{4}\:\Leftrightarrow \\ $$$$\Leftrightarrow\:\mathrm{1}×\mathrm{2}=\mathrm{2}×\mathrm{2}\:\Leftrightarrow\:\mathrm{1}=\mathrm{2}\:\Leftrightarrow\:\mathrm{1}+{n}=\mathrm{2}+{n} \\ $$$$\mathrm{i}.\mathrm{e}.\:{n}=\mathrm{1}\:\Rightarrow\:\mathrm{1}+\mathrm{1}=\mathrm{2}+\mathrm{1}\:\Leftrightarrow\:\mathrm{2}=\mathrm{3}\:\mathrm{but}\:\mathrm{1}=\mathrm{2}\:\Leftrightarrow \\ $$$$\Leftrightarrow\:\mathrm{1}+\mathrm{1}=\mathrm{2}+\mathrm{1}=\mathrm{2}+\mathrm{2}=\mathrm{4}\:… \\ $$$$\mathrm{tbis}\:\mathrm{leads}\:\mathrm{to} \\ $$$$ \\ $$$$\:\:\:\:\:\left(\mathrm{1}\right)\:{m}={n}\:\forall\:{m},\:{n}\:\in\mathbb{N} \\ $$$$ \\ $$$$\left(\mathrm{we}\:\mathrm{can}\:\mathrm{easily}\:\mathrm{expand}\:\mathrm{this}\:\mathrm{to}\:\mathbb{C}\right) \\ $$$$\Rightarrow\:\mathrm{7}×\mathrm{8}={p}\in\mathbb{N}\wedge\mathrm{7}+\mathrm{8}={q}\in\mathbb{N}\:\mathrm{and}\:\mathrm{because}\:\mathrm{of}\:\left(\mathrm{1}\right) \\ $$$$\Rightarrow\:\mathrm{7}×\mathrm{8}=\mathrm{7}+\mathrm{8}={k}\in\mathbb{N} \\ $$$$\mathrm{but}\:\mathrm{78}={h}\in\mathbb{N}\:\mathrm{and}\:\mathrm{again}\:\mathrm{using}\:\left(\mathrm{1}\right) \\ $$$$\Rightarrow\:{k}={h} \\ $$$$\Rightarrow\:\mathrm{7}×\mathrm{8}=\mathrm{7}+\mathrm{8}=\mathrm{78} \\ $$$$\mathrm{q}.\:\mathrm{e}.\:\mathrm{d}. \\ $$
Commented by Her_Majesty last updated on 08/Oct/20

$${great}! \\ $$
Commented by bemath last updated on 08/Oct/20
all calculators in the world are wrong, because the calculator calculates the result 56
Commented by Her_Majesty last updated on 08/Oct/20

$${yes}!\:{it}'{s}\:{a}\:{world}\:{wide}\:{conspiracy}\:{of}\:{the} \\ $$$${calculator}\:{industries}\:{together}\:{with}\:{the} \\ $$$${universities}…\:{they}\:{all}\:{would}\:{lose}\:{billions} \\ $$$${if}\:{the}\:{truth}\:{was}\:{reveiled}! \\ $$
Commented by MJS_new last updated on 08/Oct/20
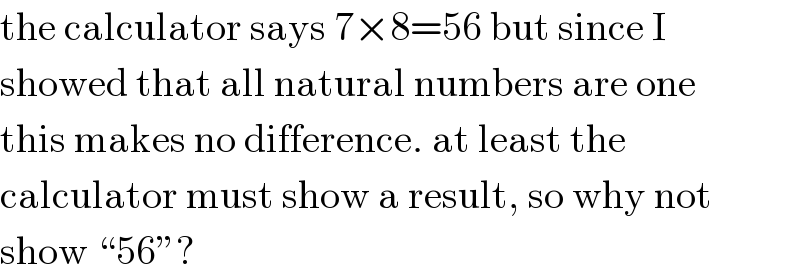
$$\mathrm{the}\:\mathrm{calculator}\:\mathrm{says}\:\mathrm{7}×\mathrm{8}=\mathrm{56}\:\mathrm{but}\:\mathrm{since}\:\mathrm{I} \\ $$$$\mathrm{showed}\:\mathrm{that}\:\mathrm{all}\:\mathrm{natural}\:\mathrm{numbers}\:\mathrm{are}\:\mathrm{one} \\ $$$$\mathrm{this}\:\mathrm{makes}\:\mathrm{no}\:\mathrm{difference}.\:\mathrm{at}\:\mathrm{least}\:\mathrm{the} \\ $$$$\mathrm{calculator}\:\mathrm{must}\:\mathrm{show}\:\mathrm{a}\:\mathrm{result},\:\mathrm{so}\:\mathrm{why}\:\mathrm{not} \\ $$$$\mathrm{show}\:“\mathrm{56}''? \\ $$
Commented by bemath last updated on 08/Oct/20
all the teachers in this world are wrong. because it teaches students 5x6 = 30 not 56
Commented by MJS_new last updated on 08/Oct/20
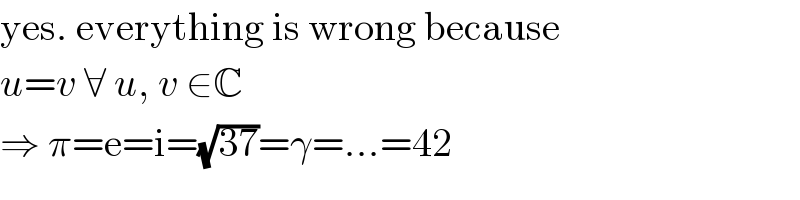
$$\mathrm{yes}.\:\mathrm{everything}\:\mathrm{is}\:\mathrm{wrong}\:\mathrm{because} \\ $$$${u}={v}\:\forall\:{u},\:{v}\:\in\mathbb{C} \\ $$$$\Rightarrow\:\pi=\mathrm{e}=\mathrm{i}=\sqrt{\mathrm{37}}=\gamma=…=\mathrm{42} \\ $$
Commented by I want to learn more last updated on 08/Oct/20

$$\mathrm{Hahahahaha} \\ $$
