Question Number 157967 by HongKing last updated on 30/Oct/21
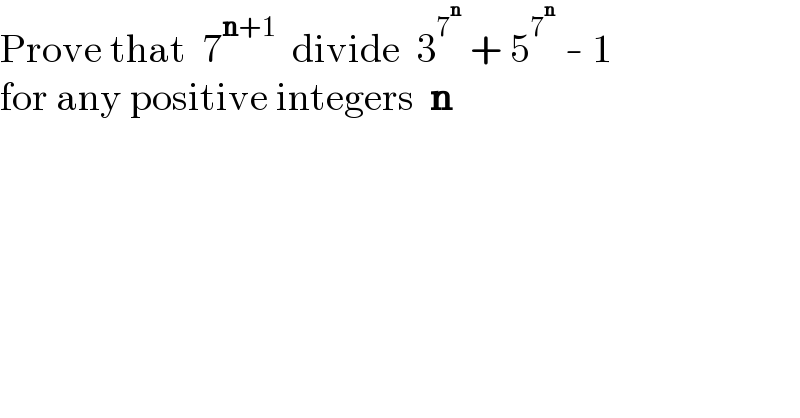
$$\mathrm{Prove}\:\mathrm{that}\:\:\mathrm{7}^{\boldsymbol{\mathrm{n}}+\mathrm{1}} \:\:\mathrm{divide}\:\:\mathrm{3}^{\mathrm{7}^{\boldsymbol{\mathrm{n}}} } \:+\:\mathrm{5}^{\mathrm{7}^{\boldsymbol{\mathrm{n}}} } \:-\:\mathrm{1} \\ $$$$\mathrm{for}\:\mathrm{any}\:\mathrm{positive}\:\mathrm{integers}\:\:\boldsymbol{\mathrm{n}} \\ $$
